Loch Ness

A smooth graph is one where the first derivative is defined at all points.  When you sketch the graph you get one continuous line with no breaks or "kinks" in it.

The modulus function, $f(x)=|x|$, is smooth apart from the point where $x=0$.  You can see that there is a "kink" when $x=0$. 
 

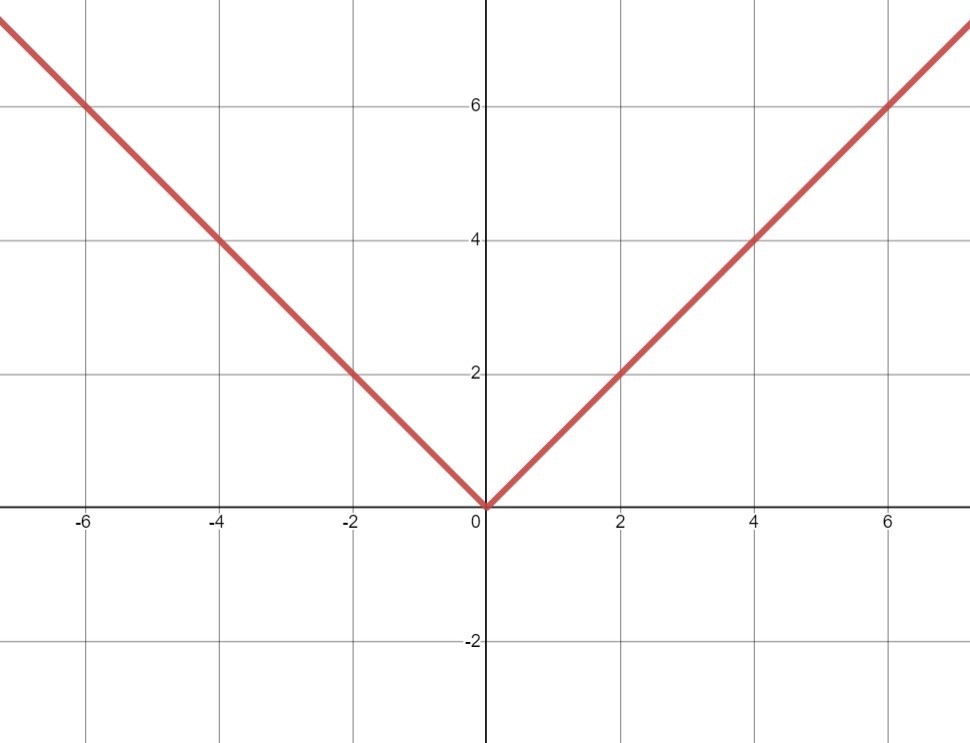
As you pass through the point the derivative changes abruptly from $-1$ to $1$.  You could write the derivative in this form:
$$\eqalign{ f'(x) &= -1 \ {\rm for } \ x<0 \cr f'(x)&= \phantom{-}1 \ {\rm for } \ x >0 .}$$

Note that $x=0$ is not included in the domain for gradient function above as $f'(x)$ is undefined when $x=0$.

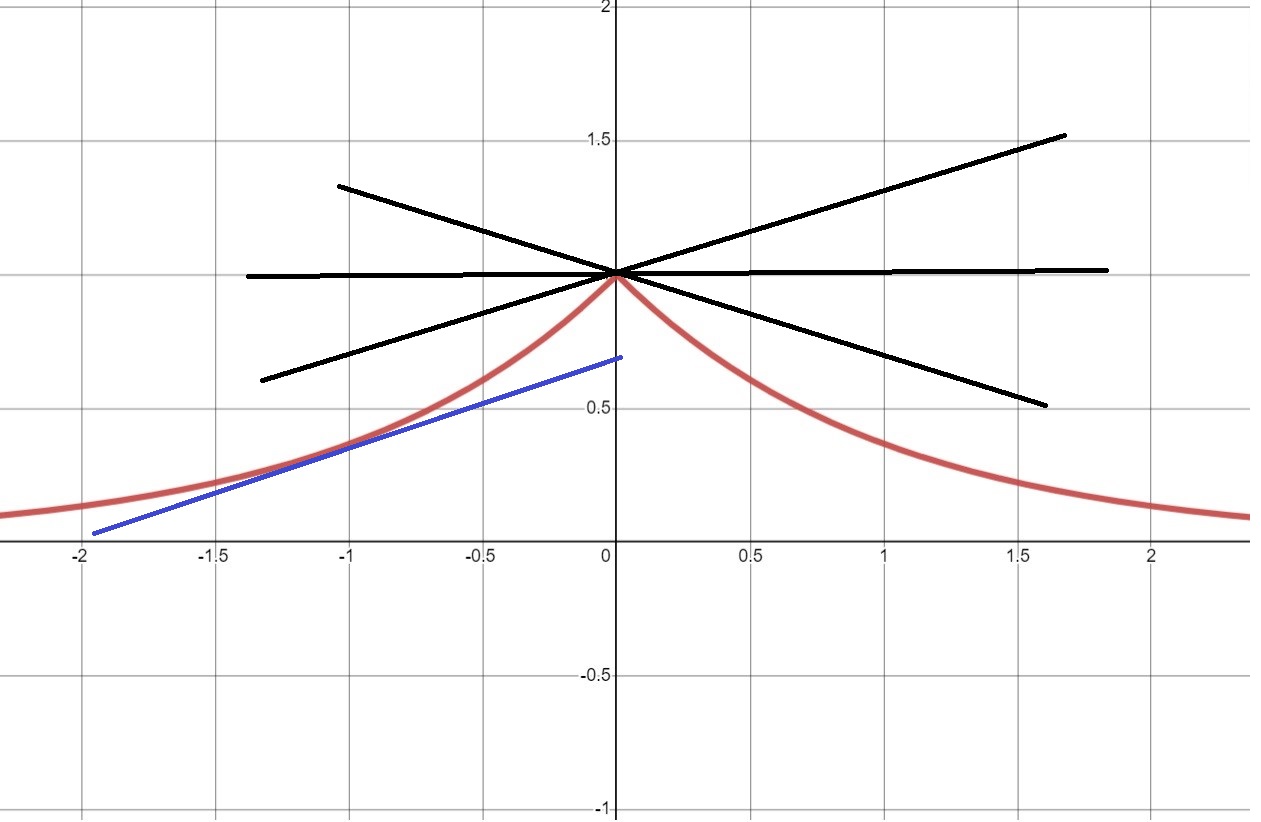
Another way of thinking about where the derivative is defined or not is whether there is a unique tangent to the curve at that point.  

The graph below is of the function $y=\text{e}^{-|x|}$. You can see that there is a "kink" when $x=0$.

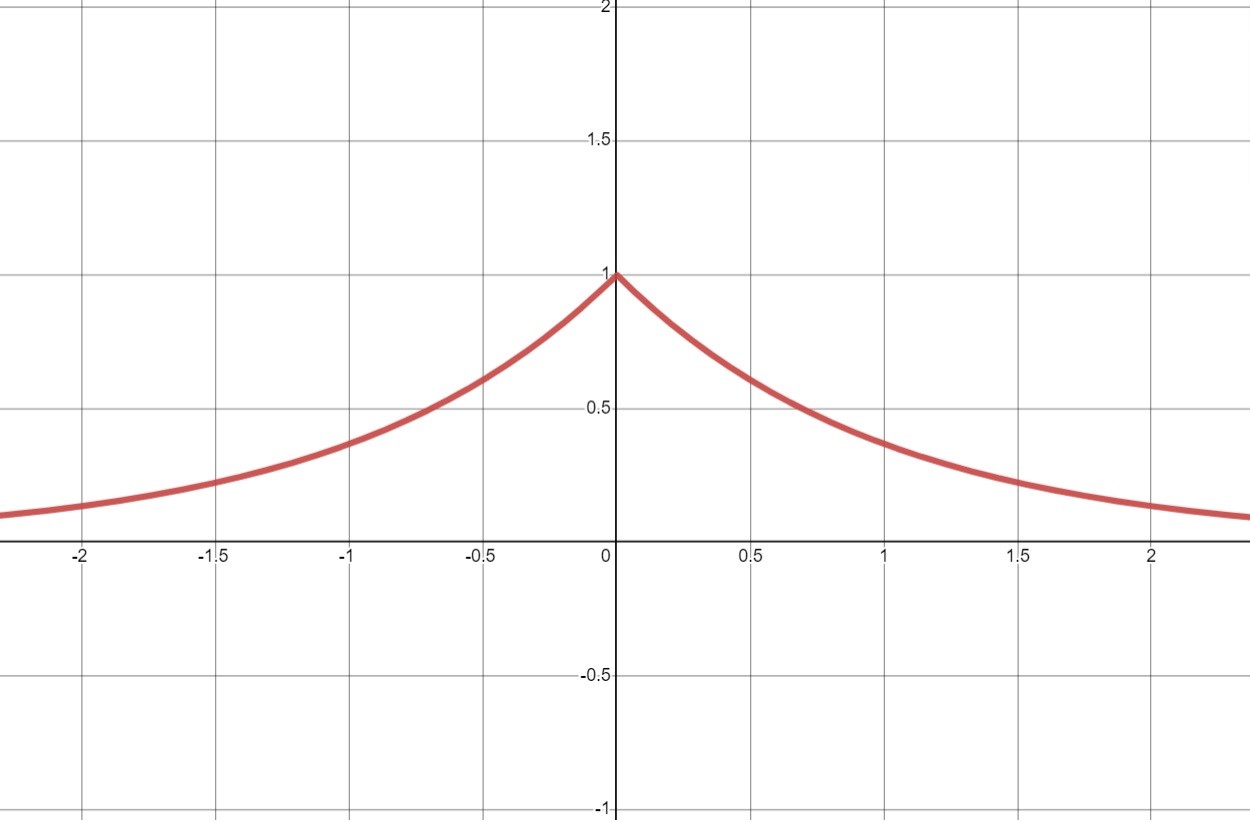
For most points on this curve there is a unique line that "touches" the curve.  At the point $(0,1)$ you can draw many possible lines that touch the curve.  There is not a "unique tangent", and the first derivative is not defined at this point.