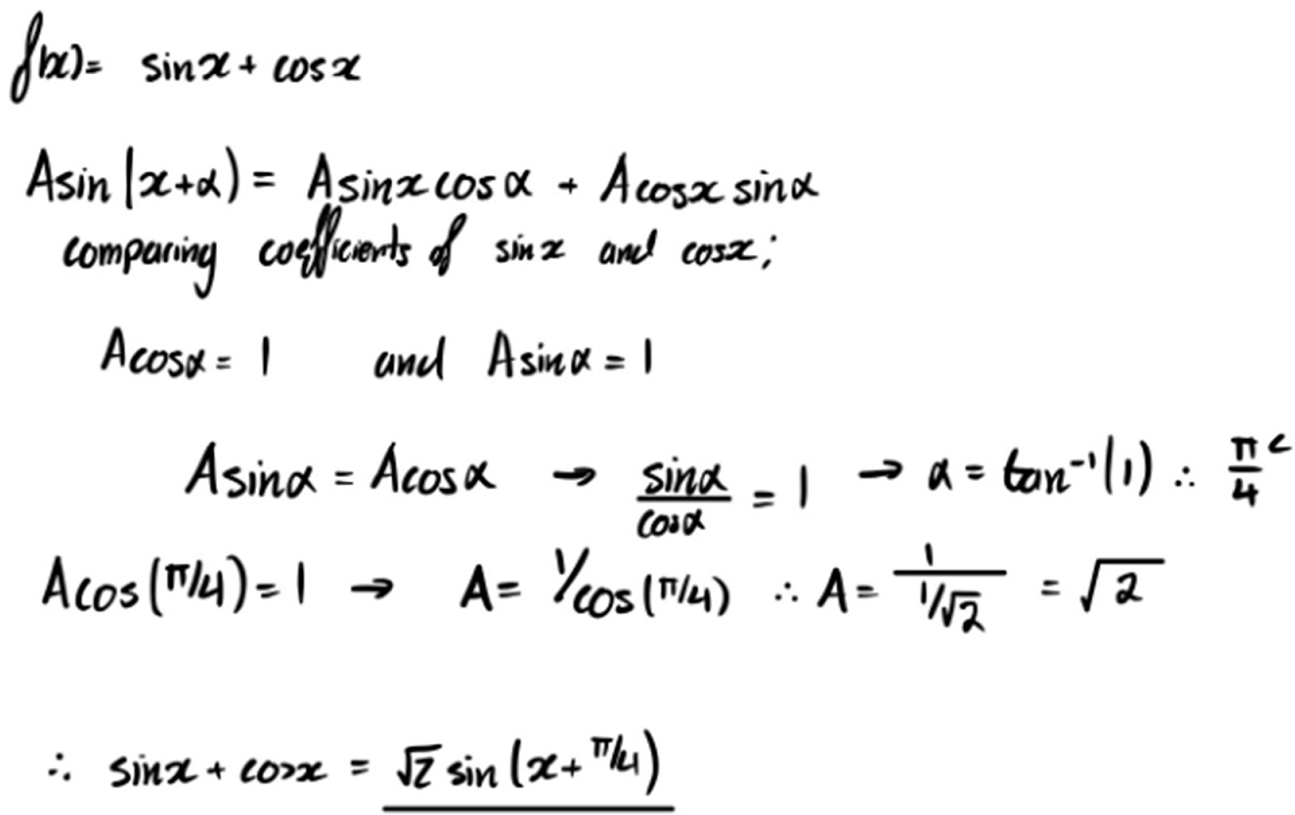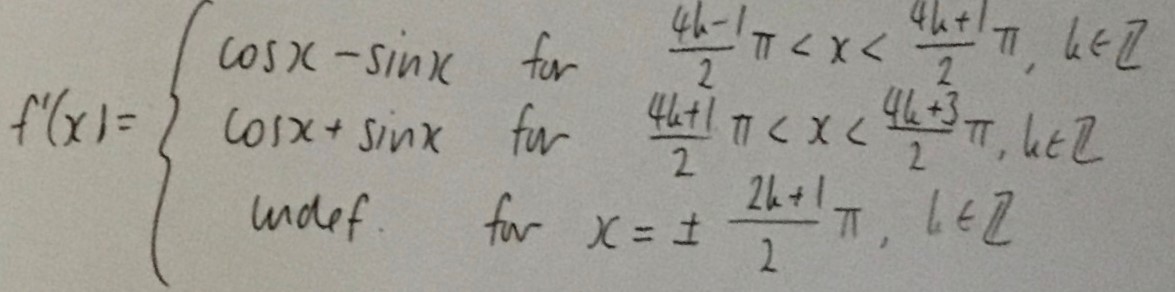Loch Ness

Dylan from Brooke Weston in the UK and Norman from Bangkok Patana School in Thailand both completed the problem correctly.

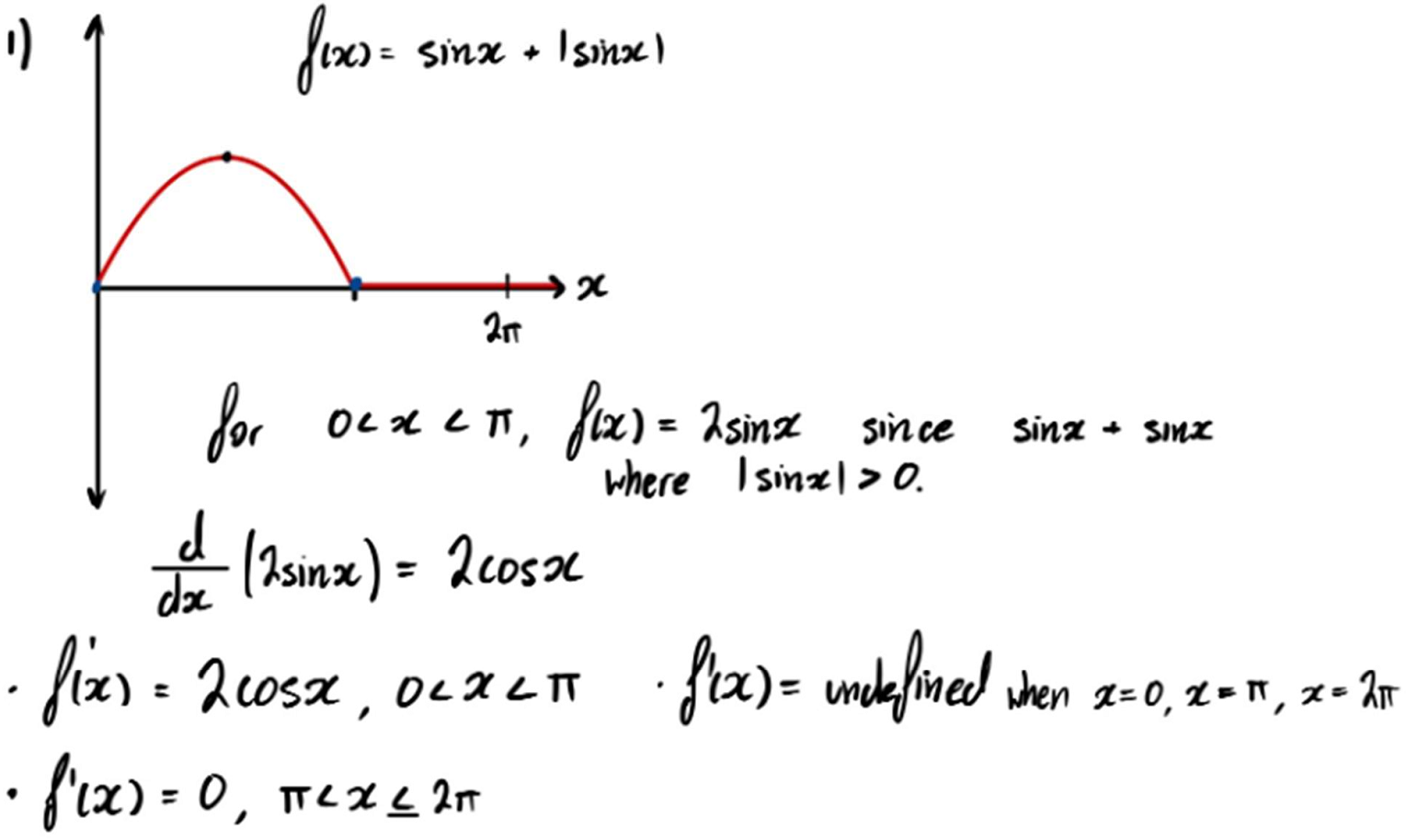
This is Norman's work on the first part of the problem, $f(x)=\sin x + |\sin x|$:

Note that the graph is actually periodic, so there is another 'hump' after $x=2\pi$. This is shown on Dylan's graph:

For the next part of the question, Dylan and Norman both expressed the $f(x)=\sin x + \cos x$ in the form $A\sin{(x+\alpha)}.$ This is Norman's work:

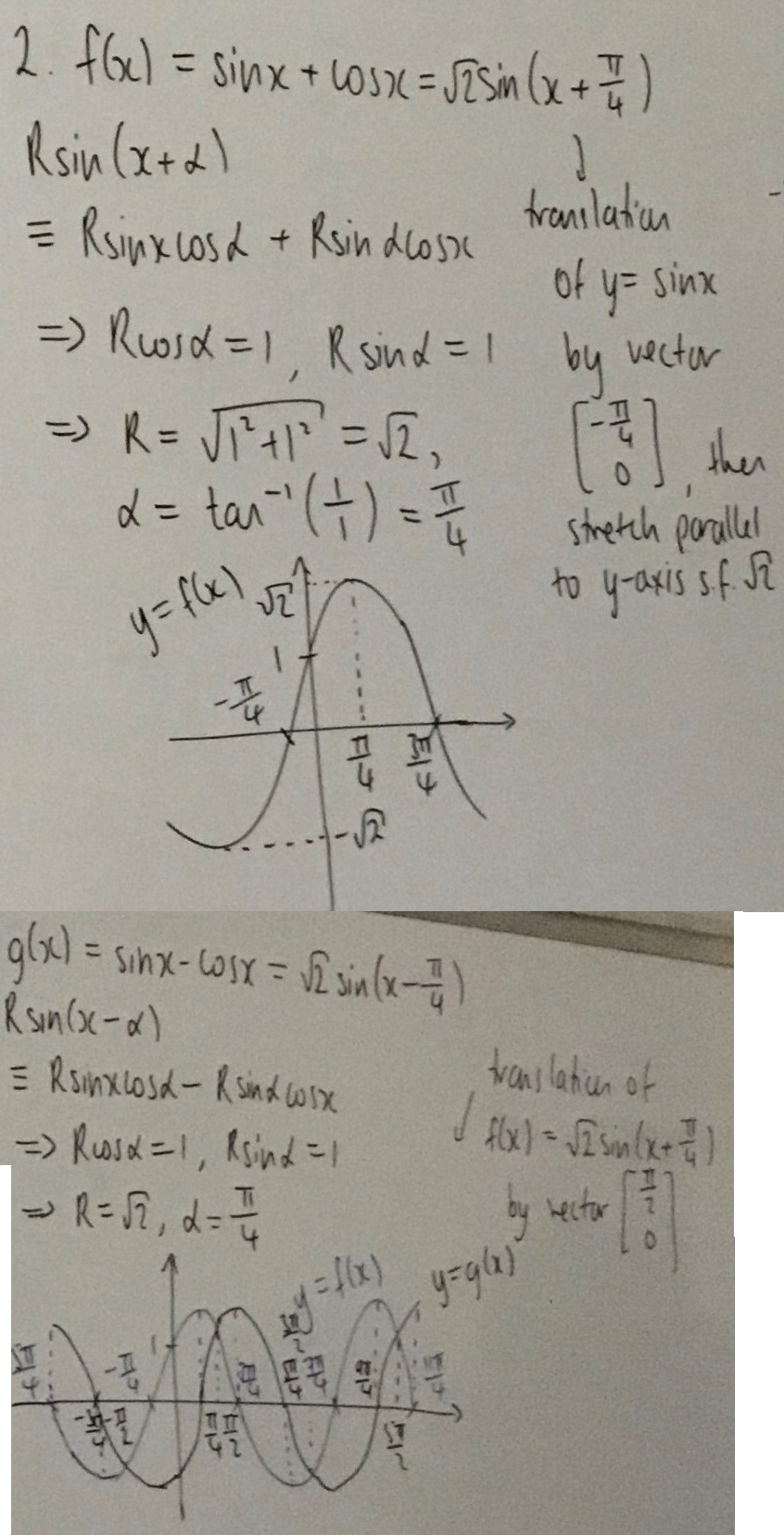
Dylan also expressed $g(x)=\sin x - \cos x$ in this form, and sketched the graphs of $y=f(x)$ and $y=g(x)$ on the same axes:

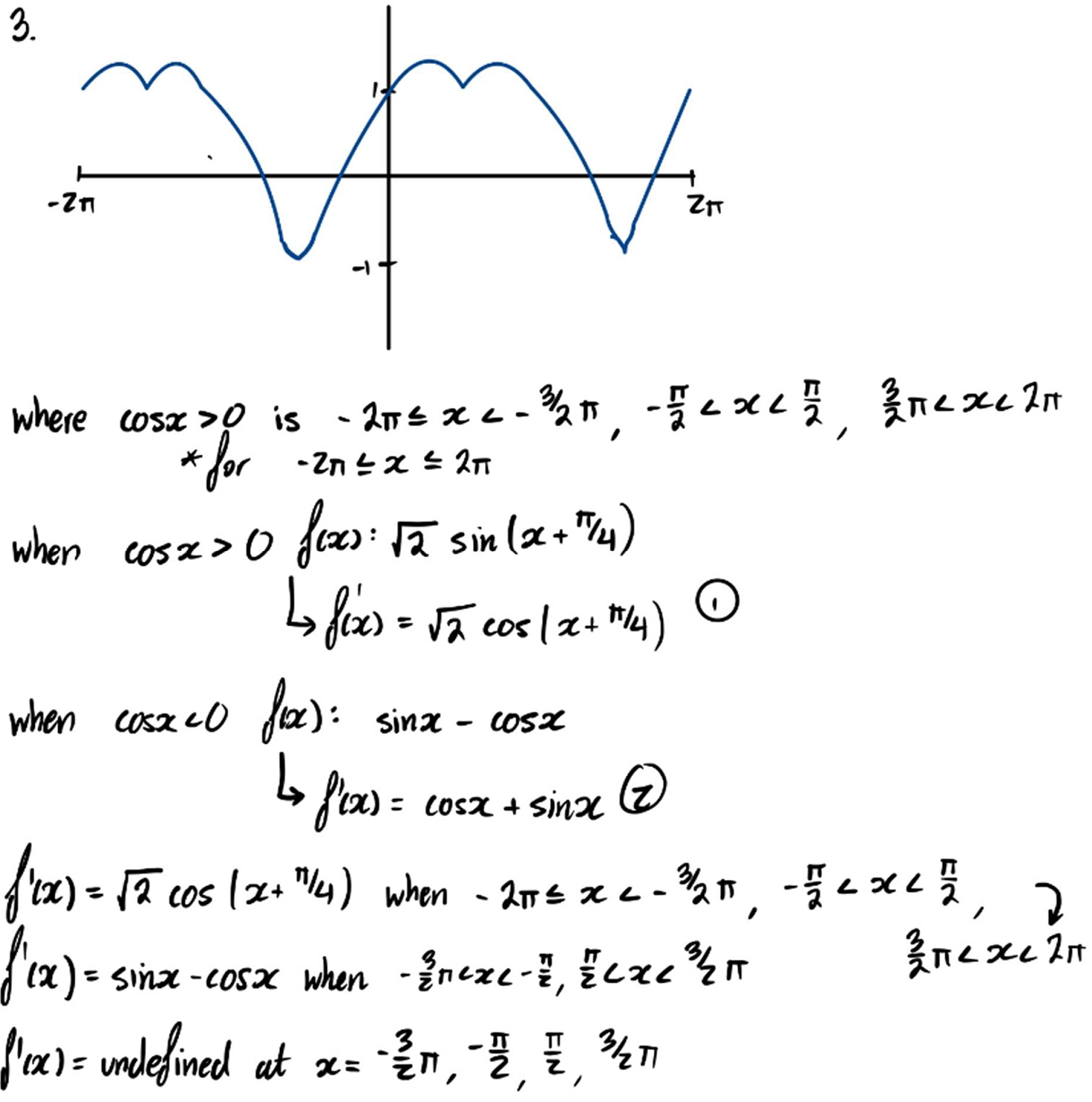
From here, Dylan and Norman sketched the graph of $y=f(x)=\sin x + |\cos x|$ and calculated the derivative $f'(x).$ This is Norman's work:

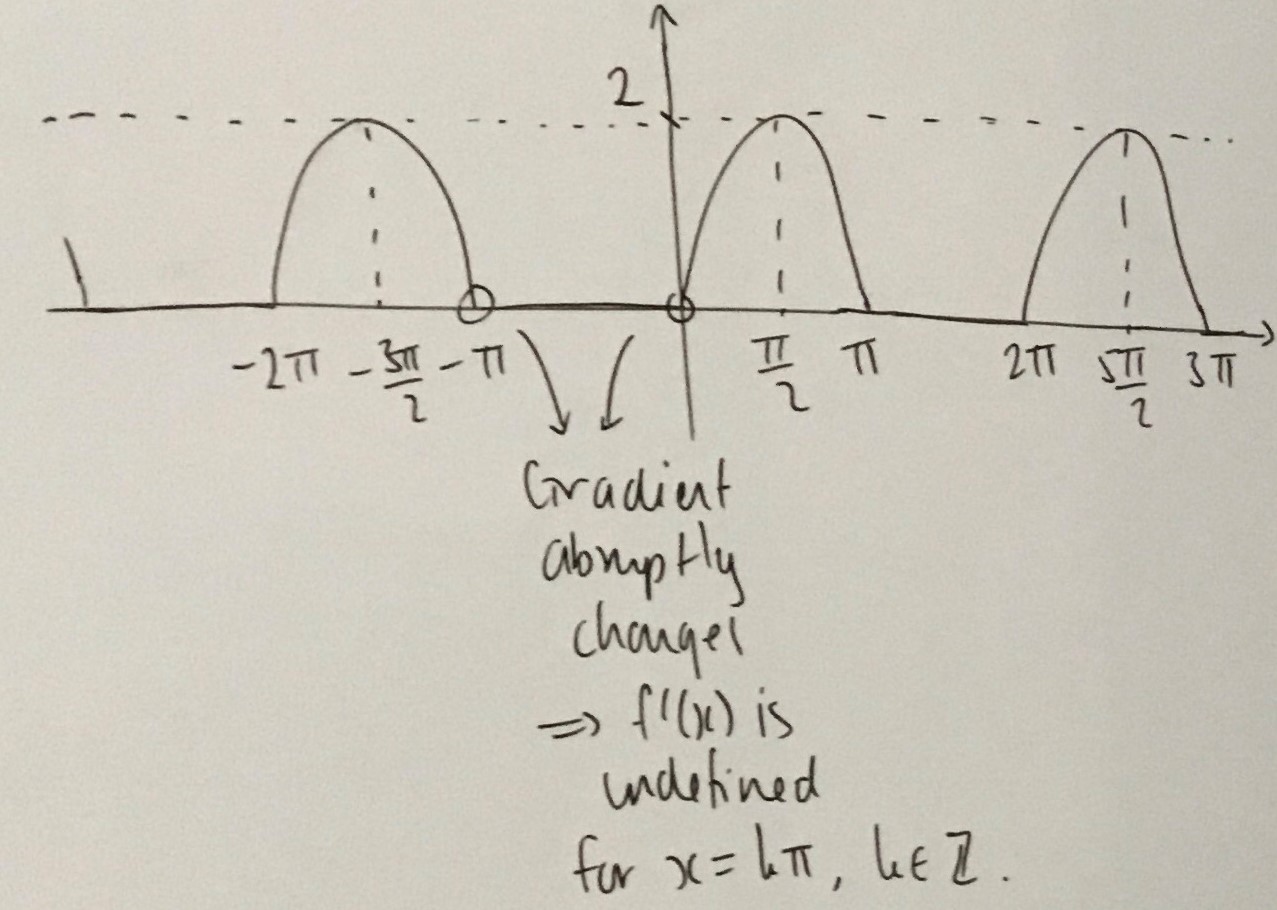
Dylan extended $f'(x)$ to include $x\lt-2\pi$ and $x\gt2\pi$: