Skip over navigation
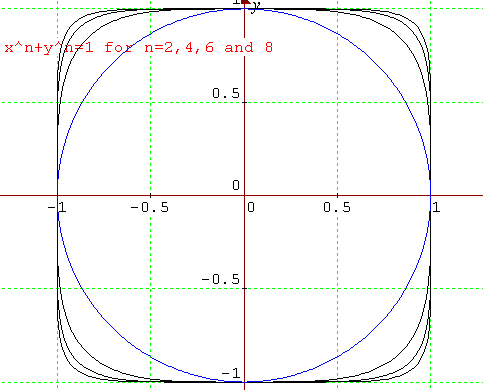
This question is about the family of relations given by $x^n+y^n=1$
(1) Explain the features of the graph of the relation $|x|+|y|=1$.
(2) Prove that $${n\over n+1} \leq {1\over 2^{1/n}} < 1 $$
(3) Consider the family of relations $x^n+y^n=1$ in the first quadrant.
Choose one particular value of $n$ and show that $y$ decreases as $x$ increases.
Show that, for each value of $n$, the graph lies entirely outside the square bounded by the lines $$x=0, \ x={n\over n+1},\ y=0,\ y={n\over n+1}$$ and inside the square bounded by the lines $$x=0,\ x=1,\ y=0,\ y=1.$$
(4) Sketch some graphs in all four quadrants of the family of relations $|x|^n+|y|^n=1$ for even values of $n$ and explain why the graphs get closer to a square shape as $n\to \infty$.
(5) Plot the graph of $x^3+y^3=1$ in all four quadrants. Why do the graphs of the relations $x^n+y^n=1$ differ according to whether $n$ is odd or even?
Squareness
Age 16 to 18
Challenge Level 
This question is about the family of relations given by $x^n+y^n=1$
(1) Explain the features of the graph of the relation $|x|+|y|=1$.
(2) Prove that $${n\over n+1} \leq {1\over 2^{1/n}} < 1 $$
(3) Consider the family of relations $x^n+y^n=1$ in the first quadrant.
Choose one particular value of $n$ and show that $y$ decreases as $x$ increases.
Show that, for each value of $n$, the graph lies entirely outside the square bounded by the lines $$x=0, \ x={n\over n+1},\ y=0,\ y={n\over n+1}$$ and inside the square bounded by the lines $$x=0,\ x=1,\ y=0,\ y=1.$$
(4) Sketch some graphs in all four quadrants of the family of relations $|x|^n+|y|^n=1$ for even values of $n$ and explain why the graphs get closer to a square shape as $n\to \infty$.
(5) Plot the graph of $x^3+y^3=1$ in all four quadrants. Why do the graphs of the relations $x^n+y^n=1$ differ according to whether $n$ is odd or even?
You may also like
Small Steps
Two problems about infinite processes where smaller and smaller steps are taken and you have to discover what happens in the limit.