Skip over navigation

Cuisenaire Counting

Age 5 to 7

Challenge Level Yellow star

Primary curriculum

Cuisenaire Counting

Cuisenaire Counting printable sheet

I have some rods that are different colours and different lengths.

I can arrange white and red rods in many different ways to be the same length as a yellow rod. Here are some of them:

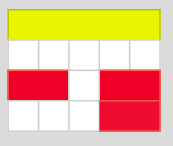
Can you find all the ways of using red and white rods that are equivalent to a yellow rod?

How will you know that you haven't missed any out?

You could use the interactivity below to try out your ideas.

The dark green rod is longer than the yellow rod.
Can you find all the ways of using red and white rods that are equivalent to a dark green rod?
How will you know that you have found them all?

Why do this problem?

This activity, offers children an environment for exploring partitioning of numbers. Ideally, learners would have real Cuisenaire rods to use, so that they can solve this problem practically as well as virtually. The activity could be used to focus on sharing strategies to find all possible solutions. These strategies can then be applied to further challenges.

Possible approach

If your children are not already familiar with Cuisenaire rods, it is essential to give them time to 'play' with the rods before having a go at this activity.

Begin the lesson by sharing the image of the yellow rod and some of the ways of making the same length using white and red rods. Try not to say anything by way of introduction or explanation, simply ask, "What do you see? What do you wonder?". Give learners a few minutes of thinking time on their own before suggesting that they talk to a partner. Invite pairs to share their noticings, or wonderings, with the whole group, writing them up on the board without offering comment yourself. Encourage members of the class to respond to anything you have written.

At this point, introduce the Cuisenaire rods, either using physical rods, or using the interactivity. If you do not have real rods, it would also be useful for students to have access to the interactivity in pairs, for example on a tablet or computer. Try to refer to the rods using their colours rather than giving them numerical values at this stage. Referring to the discussion that has already taken place (where appropriate), set up the first challenge of finding ways to arrange red and/or white rods so they are equivalent in length to a yellow rod. Ask a pupil to make an arrangement. Ask for another, different, arrangement and invite someone else to make that next to the first. Then set them off to see whether they can find other different ways, working in pairs. Can they find all the ways? How will they know they have found them all?

After a suitable length of time, draw everyone together again to talk about what they have done so far. At this stage, you may need to have a discussion about what 'different' means. Ask the group how they are making sure they don't leave out any possibilities. It could be that some learners have developed a system for creating or ordering the different ways, for example by starting with all whites, then putting in one red etc. If this isn't the case, ask pairs to draw one arrangement on a strip of paper and pin as many different arrangements as they have found on the board, or put them under a visualiser. (Alternatively, you could take screenshots of individual solutions on their devices and access these electronically on the screen.) You can then ask the children to order the arrangements by moving the strips/images. This way, it will be easier to see if they have missed any out. You could complete the solution of this part of the problem all together and then invite pupils to comment on what they might do to solve the problem if they are given a differently coloured rod (e.g. dark green) to make from reds and whites. Do they have a sense of the need for a system?

As they work on the second part of the challenge in their pairs, you will be able to listen and observe. Have they got the idea of creating possibilities in a particular order? Are they using the same order that the whole group used, or have they developed their own?

Allow time at the end of the session for children to look at what other pairs have done. It might be that this activity (and any extensions you suggest - see below) form a 'simmering' task over a period of a few days or more. Allocate a space on the wall for children to add to the possible arrangements and then come back to their contributions at a later date.

Key questions

Can you use just white rods?

Can you use just red rods?

Can you find another way to make an equivalent length to the yellow rod?

How could you put those rods in a different order to make an equivalent length to the yellow?

How will you know that you have found all the possiblities?

How could you use what you've done to help find all the possible ways for making a length equivalent to the dark green rod?

Possible extension

Some children may like to continue to work in a systematic way to find all possible ways of making lengths equivalent to a black, then brown, then blue, then orange rod from reds and whites. Alternatively, they may like to apply their method to finding all the ways of making different rod lengths using light green in addition to red and white rods.

Possible support

Children might find it helpful to use centimetre squared paper with the Cuisenaire rods for recording purposes.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Cuisenaire Counting

Cuisenaire Counting

Why do this problem?

Possible approach

Key questions

Possible extension

Possible support

You may also like

I'm Eight

Let's Investigate Triangles

Noah