An Easy Way to Multiply by 10?

Thank you to everybody who sent in their ideas about Badger's statements. Orson sent us the following explanation:

I found that Badger's solution is wrong for 0 and all decimals and fractions.

0x10=0

6.5x10=65≠6.50

1111.33358x10=11113.3358≠1111.333580

Well done for checking Badger's reasoning with some different types of numbers! Orson has used the crossed out equals sign to show that the two numbers are not equal.

What would it look like if we added a zero to the end of 0? Would it give the correct answer to the question 0x10?

Ishita and Emily from Halstead Preparatory School in the UK had similar ideas about decimals. Emily explained:

If you add 0 to the end of a number when you times by 10 or 100 or 1000... it is not always trustworthy because if you add a 0 to a decimal you could think it would be 3.50 not 35.0

Ishita said:

0 is nothing if it is at the right end of a decimal number. If you add a 0 to the right end of 6.5 it will be the same value. But if you times it by ten it has to be 10 times larger than the original number.

It looks like adding a zero to the end of a decimal isn't the same as multiplying it by ten - well done to everybody who spotted that!

I wonder what reasoning Badger could use instead that would be true for multiplying all numbers by ten?

K from Crossflatts in the UK checked each step of Badger's reasoning carefully. K explained:

1. 10 x 2 = 20 - it is true because 10 lots of 2 is 20 and 2 lots of 10 has the answer of 20 too.

2. 10 x 74 =740 - it is true:
70 x 10 =700 - I know this because 70 = 7 x 10,  and then all you have to do is multiply 70 by 10 which is 700
4 x 10 = 40 - I know 4 x 10 is 40 because I used the method for number 1 above.
So all you have to do is add them together 700 + 40 = 740.

3. 10 x 9051 = 90510 - I agree with the statement "I thought of this as ten lots of 9051, which is ten lots of 9000 added to ten lots of 51" - I used the same methods as I did above.

4. The rule will work on whole numbers but numbers with decimals might not work. e.g. 1.5 x 10 = 15 and you are not adding a 0 on.
I know this because 1 x 10 = 10 and 0.5 is half. So, 0.5 x 10 is half of 10 = 5. So 1.5 x 10 = 10 + 5 = 15. 

5. 10 x 6.5 = 6.50 - this is not true. Because 6.5 is equivalent to 6.50. So adding a zero (or any amount of zeros) doesn't make a difference to the size of the decimal. So, 10 x 6.5 = 65.

Well done for checking through all of these statements, K! I wonder why 10 x 6.5 = 65? How can we work that out?

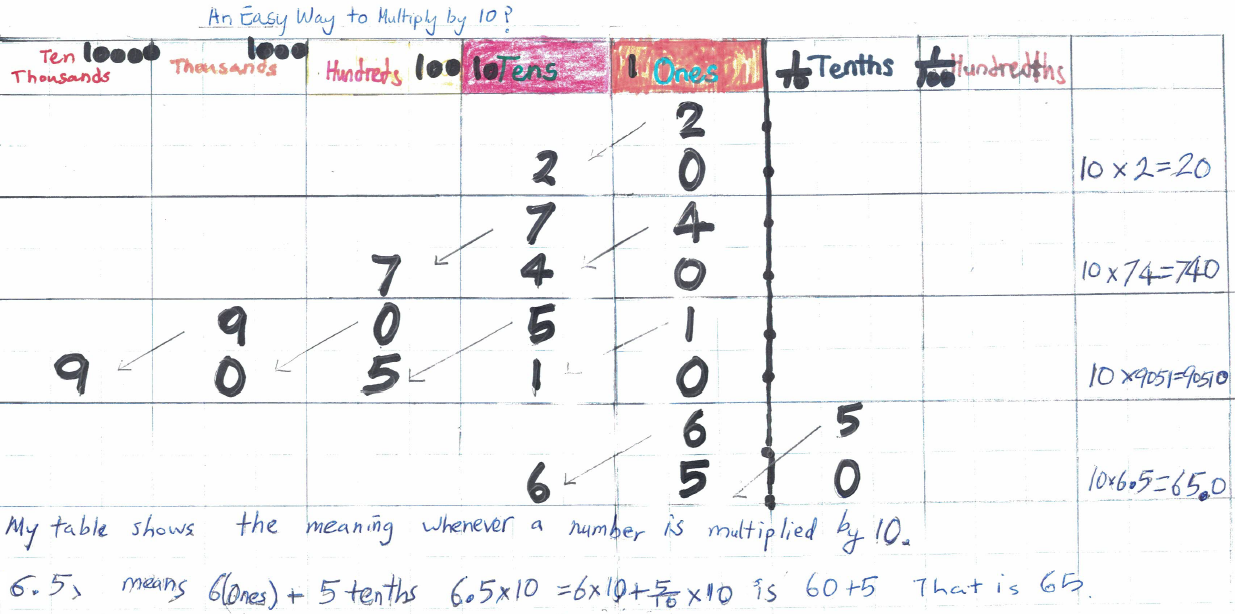
Ci Hui Minh Ngoc from Kong Hwa School in Singapore sent us the following picture to explain how to multiply by ten. You can click on the picture below to enlarge it:

This is a very clear diagram - well done! This place value grid shows that when we multiply a number by 10, the digits move one column to the left. Ci Hui Minh Ngoc has checked the answer to 6.5 x 10 by working out 6 x 10 and $\frac{5}{10}$ x 10 separately and then adding them together.

Thank you as well to Rocky from Twyford School in England and Amélie from St Nicholas CE Primary School in England, who also drew place value charts to explain how to multiply numbers by ten.