Mathdoku

Well done to everybody who solved these puzzles. We had lots of correct solutions sent in, but we've only included the solutions where children explained their reasoning for how to solve the puzzles.

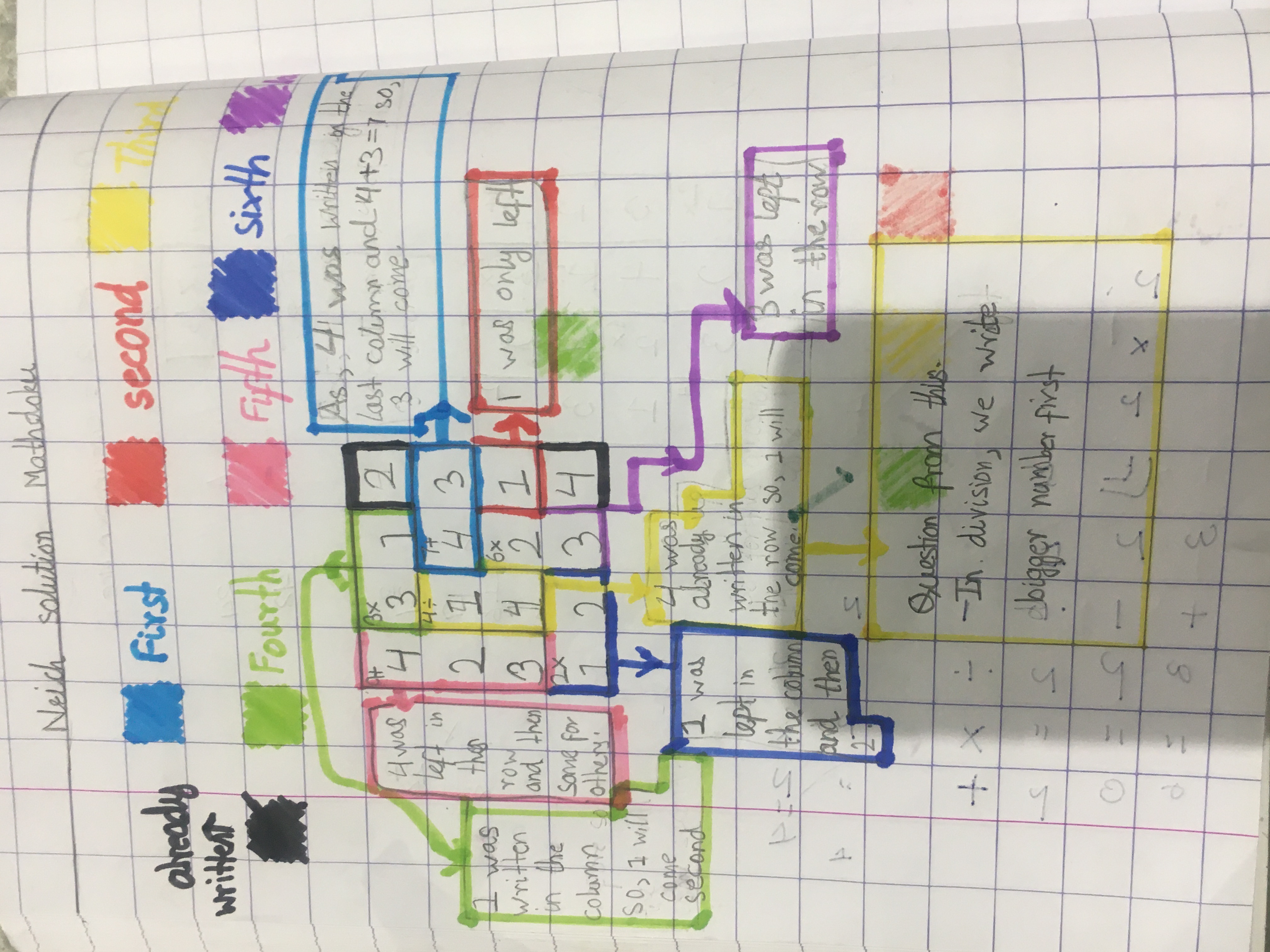
Dhruv from St Anne's Primary School in the UK sent in a picture of his solution to the first puzzle. You can click on the picture below to enlarge it:

Thank you for sending in this solution, Dhruv - it's interesting to see the order in which you filled in the cages!

Viva from Halstead Preparatory School in the UK sent in her solution to the first puzzle, and she explained how she solved this:

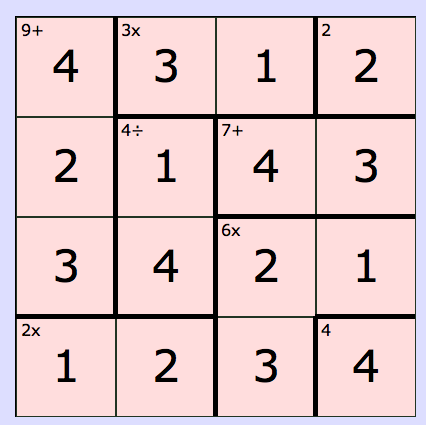
• Row 4 column 4 must be 4
• Row 1 column 4 must be 2
• Because row 4 columns 1 and 2 must be 1 or 2, column 3 must be 3
• To get a total of 7 in row 2 column 3, then row 2 column 4 must be 3 because there is already a 4 in column 4
• Therefore row 3 column 4 must be 1
• Row 3 column 3 must be a 2 (2 x 3 x 1 = 6)
• Row 1 column 3 is 1 and therefore row 1 column 2 = 3
• Row 2 column 2 must be 1 because it can’t be 4 but must be either (4 divided by 1 = 4)
• Row 4 column 2 must be 2
• Row 4 column 1 must be a 1 to get 1 x 2 = 2
• The rest of the numbers in column 1 are obvious to get the sequence for each row

Well done for writing out your reasoning step by step, Viva!

Harriet from Halstead Preparatory School gave some general advice for how to solve the puzzles:

I put the numbers in that I knew only had one square, then I worked out which numbers were possible for the other squares using the sums which were shown. When I had 3 numbers in a row, I knew which the 4th number was in any row or column.

Thank you for sharing your thoughts with us, Harriet - it's difficult to give general advice as each puzzle is so different!

Ci Hui Minh Ngoc from Kong Hwa School in Singapore sent in solutions to all of the puzzles as a PDF. Ci Hui Minh Ngoc's full solution shows how you can use the factors of a number to work out all the possibilities when the cage has a multiplication operation in the corner. Well done for solving all of these puzzles!