Chippy's Journeys

Age 7 to 11

Challenge Level Yellow star

We received lots of correct answers to the first part of this problem but very few of you told us how you went about solving it. Some of you drew a diagram of Chippy's route, which was a very good way of tackling it. Rukmini from Hopscotch Nursery and Christy, sent particularly clear pictures. Here is Rukmini's:

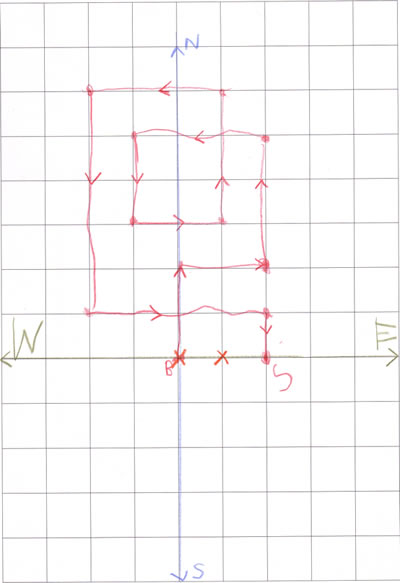
Rukmini says:

First I took some checked paper and drew a map showing North, East, West and South. In the centre was the Base station which I marked as B on the map. From B, I counted squares Chippy went along. He seemed to go a bit round and round till he forgot where the basic station was. I marked with a 'S' where he stopped. I drew his way back with crosses. He needed to go $2$ m West to get back to the Base station.

Tom who lives in New Zealand, solved the the first part of problem in a different, but equally as good way. Here is what Tom says:

This is a table showing how many metres Chippy went:

	N	S	E	W
	2	2	2	3
	3	5	2	3
	3	1	4
Total	8	8	8	6

The north and the south amounts were the same so there was no change there, but the east and the west amounts were different. The east was $2$ metres more than the west. So you have to go $2$ metres in west at the end to get to Chippy's station.

Well done to you all for your well explained solutions.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Chippy's Journeys

You may also like

Great Squares

Watch the Clock

Walk and Ride