Skip over navigation
The Golden Ratio is one of the roots of the equation $x^2-x-1=0$ and the $n$th Fibonacci number is$F_n={1\over\sqrt5}(\alpha^n-\beta^n)$ where $\alpha$ and $\beta$ are solutions of the quadratic equation $x^2-x-1=0$ and $\alpha > \beta$ hence the many connections between Fibonacci numbers and the Golden Ratio.
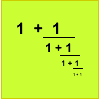

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Plus or Minus
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
The Golden Ratio is one of the roots of the equation $x^2-x-1=0$ and the $n$th Fibonacci number is$F_n={1\over\sqrt5}(\alpha^n-\beta^n)$ where $\alpha$ and $\beta$ are solutions of the quadratic equation $x^2-x-1=0$ and $\alpha > \beta$ hence the many connections between Fibonacci numbers and the Golden Ratio.
You may also like
Continued Fractions I
An article introducing continued fractions with some simple puzzles for the reader.
Fibonacci Factors
For which values of n is the Fibonacci number fn even? Which Fibonnaci numbers are divisible by 3?

