Skip over navigation
This solution is from Andrei from Tudor Vianu National College, Bucharest, Romania. Calculating $F_1$, $F_2,. . . , F_7$, I obtain: $$F_1 = 1;\ F_2 = 1;\ F_3 = 2;\ F_4 =3;\ F_5 = 5;\ F_6 = 8;\ F_7 = 13.$$ Calculating $F_{n-1}F_{n+1}$ for some values of $n$: \begin{eqnarray} n = 2: F_1F_3 &= 2 = 1 + 1 = (F_2)^2 + 1 \\ n = 3: F_2F_4 &= 3 = 4 - 1 = (F_3)^2 - 1 \\ n = 4: F_3F_5 &= 10 = 9 + 1 = (F_4)^2 + 1 \\ n = 5: F_4F_6 &= 24 = 25 - 1 = (F_5)^2 - 1 \\ n = 6: F_5F_7 &=65 = 64 + 1 = (F_6)^2 + 1 . \end{eqnarray} Observing this, I try to prove the conjecture that: $$F_{n-1}F_{n+1}= (F_n)^2 + (-1)^n.$$ Using the general formula for $F_{n-1}$ and $F_{n+1}$ in terms of $\alpha$ and $\beta$, the roots of the equation $x^2-x-1=0$, I find: \begin{eqnarray} F_{n-1}F_{n+1} &= {1\over 5}(\alpha^{n-1}-\beta^{n-1})(\alpha^{n+1}-\beta^{n+1}) \\ &= {1\over 5}[ \alpha ^{2n} + \beta^{2n}-(\alpha^2+\beta^2)(\alpha\beta)^{n-1}] \\ &= {1\over 5}[(\alpha^n-\beta^n)^2+ 2(\alpha\beta)^n -(\alpha^2+\beta^2)(\alpha\beta)^{n-1}] \\ &= F_n^2 -{1\over 5}(\alpha\beta)^{n-1}(\alpha-\beta)^2 . \end{eqnarray} At this point we use the fact that $\alpha\beta=-1$ and $\alpha-\beta=\sqrt 5$ which gives the result $$F_{n+1}F_{n-1}=F_n^2 +(-1)^n$$ thus proving the conjecture.
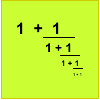

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Plus or Minus
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This solution is from Andrei from Tudor Vianu National College, Bucharest, Romania. Calculating $F_1$, $F_2,. . . , F_7$, I obtain: $$F_1 = 1;\ F_2 = 1;\ F_3 = 2;\ F_4 =3;\ F_5 = 5;\ F_6 = 8;\ F_7 = 13.$$ Calculating $F_{n-1}F_{n+1}$ for some values of $n$: \begin{eqnarray} n = 2: F_1F_3 &= 2 = 1 + 1 = (F_2)^2 + 1 \\ n = 3: F_2F_4 &= 3 = 4 - 1 = (F_3)^2 - 1 \\ n = 4: F_3F_5 &= 10 = 9 + 1 = (F_4)^2 + 1 \\ n = 5: F_4F_6 &= 24 = 25 - 1 = (F_5)^2 - 1 \\ n = 6: F_5F_7 &=65 = 64 + 1 = (F_6)^2 + 1 . \end{eqnarray} Observing this, I try to prove the conjecture that: $$F_{n-1}F_{n+1}= (F_n)^2 + (-1)^n.$$ Using the general formula for $F_{n-1}$ and $F_{n+1}$ in terms of $\alpha$ and $\beta$, the roots of the equation $x^2-x-1=0$, I find: \begin{eqnarray} F_{n-1}F_{n+1} &= {1\over 5}(\alpha^{n-1}-\beta^{n-1})(\alpha^{n+1}-\beta^{n+1}) \\ &= {1\over 5}[ \alpha ^{2n} + \beta^{2n}-(\alpha^2+\beta^2)(\alpha\beta)^{n-1}] \\ &= {1\over 5}[(\alpha^n-\beta^n)^2+ 2(\alpha\beta)^n -(\alpha^2+\beta^2)(\alpha\beta)^{n-1}] \\ &= F_n^2 -{1\over 5}(\alpha\beta)^{n-1}(\alpha-\beta)^2 . \end{eqnarray} At this point we use the fact that $\alpha\beta=-1$ and $\alpha-\beta=\sqrt 5$ which gives the result $$F_{n+1}F_{n-1}=F_n^2 +(-1)^n$$ thus proving the conjecture.
You may also like
Continued Fractions I
An article introducing continued fractions with some simple puzzles for the reader.
Fibonacci Factors
For which values of n is the Fibonacci number fn even? Which Fibonnaci numbers are divisible by 3?

