Triangle Pin-down

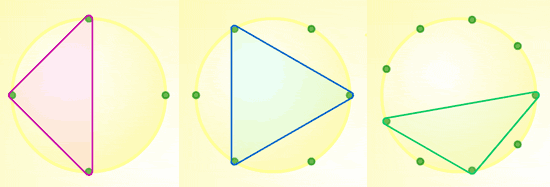
A right-angled triangle has been drawn on the four-pin board above left.

Can you draw the same type of triangle on a three-pin board?

How many pins could there be on the board for you to be able to draw the same type of triangle?

Do you notice anything about the number of pins for which this is possible?

What kind of triangle is drawn on the six-pin board above?

How many pins could there be on the board for you to be able to draw the same type of triangle?

Do you notice anything about the number of pins for which this is possible?

Can you name the type of triangle drawn on the nine-pin board above?

On what size board could you draw the same type of triangle?

Do you notice anything about the number of pins for which this is possible?

You might like to use the interactivity to try out your ideas.
Once you have chosen the number of dots you need, select the line drawing tool. Click on two points to draw a line between them.



For printable sets of circle templates for use with this activity, please see Printable Resources page.

Many thanks to Geoff Faux who introduced us to the merits of the 9 pin circular geoboard.

For further ideas about using geoboards in the classroom, please see Geoff's publications available through the Association of Teachers of Mathematics (search for 'geoboards').