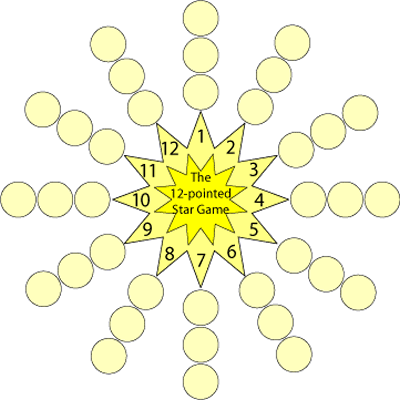
The Twelve Pointed Star Game

This game is for two or more players.

You will need a copy of the star board, counters and two 1-6 dice.

Each player chooses three numbers on the star. (If you play with more than four players, each player chooses two numbers.)
Players then take it in turns to roll two dice and add the scores.
The player who has chosen that number puts a counter on the appropriate circle. 

The winner is the first player to have counters on all three circles belonging to one of their chosen numbers.

For example I'm playing with my friend Zac. I choose the numbers 2, 4 and 6; Zac chooses 7, 8 and 9.
Zac rolls the dice and it's a 4 and a 2, which makes a total of 6.
This means I can put a counter on one of the circles next to the 6.

Play the game a few times.

Which are good numbers to choose? Why?
Which are poor numbers to choose? Why?
Which is the worst number to choose? Why?