Skip over navigation
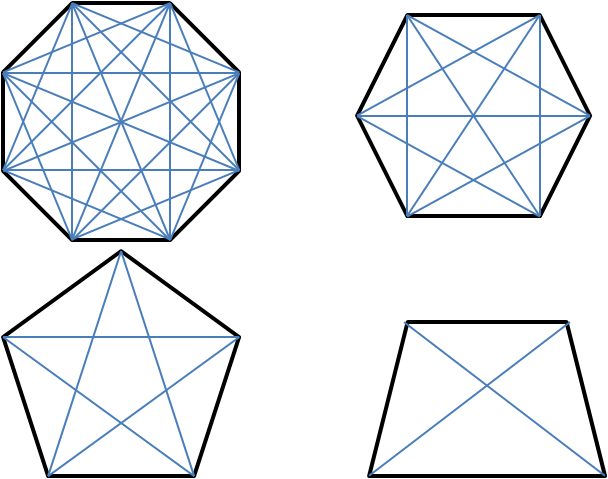Drawing the diagonals for each of the shapes and counting shows that an octagon has $20$ diagonals, a hexagon has $9$, a pentagon has $5$ and a quadrilateral has $2$.
This can be used to show that A to D are all correct. A quadrilateral has half as many diagonals as it has sides, not twice as many, so statement E is false.
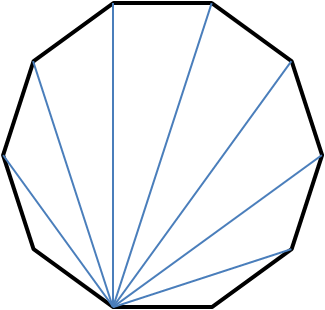Alternatively, each vertex in a polygon shares a diagonal with $n-3$ others, if there are $n$ vertices, since it does not share one with itself or either of its neighbours. There are $n$ vertices, so this is $n(n-3)$. But this means we have counted each diagonal twice, so there are
$\frac 12 n(n-3)$ in total. This gives the numbers obtained directly above.
Bishop's Paradise
Age 11 to 14
ShortChallenge Level 
Drawing the diagonals for each of the shapes and counting shows that an octagon has $20$ diagonals, a hexagon has $9$, a pentagon has $5$ and a quadrilateral has $2$.This can be used to show that A to D are all correct. A quadrilateral has half as many diagonals as it has sides, not twice as many, so statement E is false.
Alternatively, each vertex in a polygon shares a diagonal with $n-3$ others, if there are $n$ vertices, since it does not share one with itself or either of its neighbours. There are $n$ vertices, so this is $n(n-3)$. But this means we have counted each diagonal twice, so there are
$\frac 12 n(n-3)$ in total. This gives the numbers obtained directly above.This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Is There a Theorem?
Draw a square. A second square of the same size slides around the first always maintaining contact and keeping the same orientation. How far does the dot travel?