Skip over navigation
Suppose that a and b are natural numbers. If $\sqrt{a} + \sqrt{b}$ is rational then show that it is a natural number. Show that, indeed both $\sqrt{a}$ and $\sqrt{b}$ are then integers.
Suppose that a, b and c are natural numbers. If $\sqrt{a} + \sqrt{b} + \sqrt{c}$ is rational then show that it is a natural number. Moreover show that $\sqrt{a}$ , $\sqrt{b}$ and $\sqrt{c}$ are then integers.
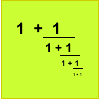
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Rational Roots
Age 16 to 18
Challenge Level 





Suppose that a and b are natural numbers. If $\sqrt{a} + \sqrt{b}$ is rational then show that it is a natural number. Show that, indeed both $\sqrt{a}$ and $\sqrt{b}$ are then integers.
Suppose that a, b and c are natural numbers. If $\sqrt{a} + \sqrt{b} + \sqrt{c}$ is rational then show that it is a natural number. Moreover show that $\sqrt{a}$ , $\sqrt{b}$ and $\sqrt{c}$ are then integers.
You may also like
Good Approximations
Solve quadratic equations and use continued fractions to find rational approximations to irrational numbers.

