Skip over navigation
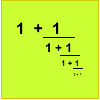

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Be Reasonable
Age 16 to 18
Challenge Level 





Prove that there is no arithmetic progression containing all three of $\sqrt{2}$, $\sqrt{3}$ and $\sqrt{5}$.
You may also like
Good Approximations
Solve quadratic equations and use continued fractions to find rational approximations to irrational numbers.
Rational Roots
Given that a, b and c are natural numbers show that if sqrt a+sqrt b is rational then it is a natural number. Extend this to 3 variables.

