Skip over navigation
Why do this problem?
It is an exercise in proof by contradiction.
Possible approach
First discuss proof by contradiction so that students appreciate how the logic of arguments by contradiction work. You can draw on this article on Proof by Contradiction.
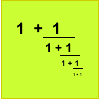

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Be Reasonable
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
It is an exercise in proof by contradiction.
Possible approach
First discuss proof by contradiction so that students appreciate how the logic of arguments by contradiction work. You can draw on this article on Proof by Contradiction.
Then discuss the proof that $\sqrt 2$ is irrational.
The students can work with the interactivity
Proof Sorter and perhaps some of them might read
this article which was written by two undergraduates.
Key Question
If the difference between$\sqrt 2$ and $\sqrt 3$ is an integer
multiple of the common difference in an arithmetic series, and the
difference between $\sqrt 3$ and $\sqrt 5$ is also an integer
multiple of that common difference, can you use these two facts to
write down two expressions, eliminate the unknown common difference
and then find an impossible relationship?
Possible support
Proof Sorter and
article
Possible
extension
Can you prove that $\sqrt{1}$, $\sqrt{2}$ and $\sqrt{3}$
cannot be terms of ANY arithmetic progression?
You may also like
Good Approximations
Solve quadratic equations and use continued fractions to find rational approximations to irrational numbers.
Rational Roots
Given that a, b and c are natural numbers show that if sqrt a+sqrt b is rational then it is a natural number. Extend this to 3 variables.

