Skip over navigation
Triangle Incircle Iteration
Age 14 to 16
Challenge Level 
Why do this problem?
This problem leads to a result which is easy to guess visually
but not so easy to prove.
Geometrical, numerical, and algebraic ideas can all be used to
reach a solution, and properties of averaging can also come out of
the problem. Numerical patterns can be investigated using a
spreadsheet.Possible approach
Use the interactivity (or accurately construct some triangles
with their inscribed circles) and see what happens to the angles in
the nested triangles.In order to see why this is happening, it's
important to make sure everyone knows that the centre of the
inscribed circle is at the point where the angle bisectors of the
original triangle meet, and that radii meet tangents at a right
angle. This information can be used to write expressions for the
three angles in the new triangle in terms of the original
angles.
Students could now create a spreadsheet which allows them to
input three angles which sum to 180 degrees and use their
expressions to work out the three new angles. By continuing the
sequence, the angles quickly converge.
Key questions
What seems to be happening to the angles in each new triangle
that we draw?
How can we calculate the angles of each new triangle if we
know the original angles?
Possible extension
Investigate the sequence $(90-x/2), 90-(90-x/2)/2$ and so on
to explain why the angles converge to their limit.
The three new angles are each the mean of a pair of the
original angles. In general, what happens if you keep finding the
mean of pairs of numbers to give three new numbers?
Possible support
Work with numerical examples and try to explain the patterns formed.You may also like
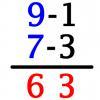
Vedic Sutra - All from 9 and Last from 10
Vedic Sutra is one of many ancient Indian sutras which involves a cross subtraction method. Can you give a good explanation of WHY it works?
Tournament Scheduling
Scheduling games is a little more challenging than one might desire. Here are some tournament formats that sport schedulers use.
Archimedes and Numerical Roots
The problem is how did Archimedes calculate the lengths of the sides of the polygons which needed him to be able to calculate square roots?