Skip over navigation
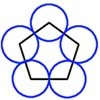
Look for angles which will help you to show that the angles in question are $180^{\circ}$ so the lines are straight.
Circumspection
Age 14 to 16
Challenge Level 
Look for angles which will help you to show that the angles in question are $180^{\circ}$ so the lines are straight.
You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Polycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?
Quadarc
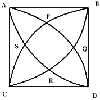
Given a square ABCD of sides 10 cm, and using the corners as centres, construct four quadrants with radius 10 cm each inside the square. The four arcs intersect at P, Q, R and S. Find the area enclosed by PQRS.