Skip over navigation
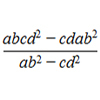

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Novemberish
Age 14 to 16
Challenge Level 





- Problem
- Student Solutions

(a) A four digit number (in base $10$) $aabb$ is a perfect
square. Discuss ways of systematically finding this number.
(b) Prove that $11^{10}-1$ is divisible by $100$.
You may also like
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.
2-digit Square
A 2-Digit number is squared. When this 2-digit number is reversed and squared, the difference between the squares is also a square. What is the 2-digit number?

