Skip over navigation
Square World
Age 16 to 18
Challenge Level 
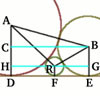
| $P$ is a point inside a square $ABCD$ such that $PA= 1$, $PB = 2$ and $PC = 3$. How big is ${\angle APB} $ ? |
 |
You may also like
Baby Circle
A small circle fits between two touching circles so that all three circles touch each other and have a common tangent? What is the exact radius of the smallest circle?
Logosquares
Ten squares form regular rings either with adjacent or opposite vertices touching. Calculate the inner and outer radii of the rings that surround the squares.
Two Trees
Two trees 20 metres and 30 metres long, lean across a passageway between two vertical walls. They cross at a point 8 metres above the ground. What is the distance between the foot of the trees?