Skip over navigation
Thank you to Isabelle from Maidstone Grammar School for Girls who sent a correct solution for the completed square. Andrew, Brian, Dylan and Maroun from Greenacre Public School in Australia and Lawrence from the UK sent in very similar solutions that were clearly explained. This is Lawrence's solution:
1. We started off by thinking about what digit could go in the top LH corner (A,N) and soon realised that it had to be 1 otherwise the multiple of 6 would not fit in the table.
2. We then looked at the RH column and realised that as 5N would have to end in 5 or 0, the only place a 1 could go in the RH column was the only other odd multiple left, which was 3 (F,3).
The only number to give a multiple ending in 1 is 3 x 7, so (F,N) was 7, and we were then able to fill in the rest of column F and carry the 10s over into column E.
3. Now that we had all the digits we went back to column A and put the digits in, in numerical order (checking that it was feasible), which allowed us to work out that (B, N) was 4.
4. We then used trial and error to put the remaining 3 digits of N in starting at the RHS of the table and working down each column.
We only realised when we had finished that there is a pattern in the rows, i.e. the digits are always in the same order: 1, 4, 2, 8, 5, 7.
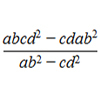


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Latin Numbers
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Thank you to Isabelle from Maidstone Grammar School for Girls who sent a correct solution for the completed square. Andrew, Brian, Dylan and Maroun from Greenacre Public School in Australia and Lawrence from the UK sent in very similar solutions that were clearly explained. This is Lawrence's solution:
1. We started off by thinking about what digit could go in the top LH corner (A,N) and soon realised that it had to be 1 otherwise the multiple of 6 would not fit in the table.
2. We then looked at the RH column and realised that as 5N would have to end in 5 or 0, the only place a 1 could go in the RH column was the only other odd multiple left, which was 3 (F,3).
The only number to give a multiple ending in 1 is 3 x 7, so (F,N) was 7, and we were then able to fill in the rest of column F and carry the 10s over into column E.
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| N | 1 | 7 | ||||
| 2N | 4 | |||||
| 3N | 1 | |||||
| 4N | 8 | |||||
| 5N | 5 | |||||
| 6N | 2 |
3. Now that we had all the digits we went back to column A and put the digits in, in numerical order (checking that it was feasible), which allowed us to work out that (B, N) was 4.
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| N | 1 | 4 | 7 | |||
| 2N | 2 | 4 | ||||
| 3N | 4 | 1 | ||||
| 4N | 5 | 8 | ||||
| 5N | 7 | 5 | ||||
| 6N | 8 | 2 |
4. We then used trial and error to put the remaining 3 digits of N in starting at the RHS of the table and working down each column.
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| N | 1 | 4 | 2 | 8 | 5 | 7 |
| 2N | 2 | 8 | 5 | 7 | 1 | 4 |
| 3N | 4 | 2 | 8 | 5 | 7 | 1 |
| 4N | 5 | 7 | 1 | 4 | 2 | 8 |
| 5N | 7 | 1 | 4 | 2 | 8 | 5 |
| 6N | 8 | 5 | 7 | 1 | 4 | 2 |
We only realised when we had finished that there is a pattern in the rows, i.e. the digits are always in the same order: 1, 4, 2, 8, 5, 7.
You may also like
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.
Novemberish
a) A four digit number (in base 10) aabb is a perfect square. Discuss ways of systematically finding this number. (b) Prove that 11^{10}-1 is divisible by 100.
2-digit Square
A 2-Digit number is squared. When this 2-digit number is reversed and squared, the difference between the squares is also a square. What is the 2-digit number?

