Skip over navigation

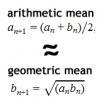
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Stretching Fractions
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
What is the routine for calculating the result when the
fraction is less than or equal to a half ?
What is the routine when the fraction is greater than a
half?
Can you express that in algebra?
If $x$ is the fraction value what is the result in terms of
$x$ for the two cases above?
For each denominator (bottom number of the fraction) which
fractions are equivalent to other fractions with a smaller
denominator?
Which fractions form a loop?
Which fractions do not belong to the loop but track into
it?
You may also like
Triangle Incircle Iteration
Keep constructing triangles in the incircle of the previous triangle. What happens?
Loopy
Investigate sequences given by $a_n = \frac{1+a_{n-1}}{a_{n-2}}$ for different choices of the first two terms. Make a conjecture about the behaviour of these sequences. Can you prove your conjecture?
Converging Means
Take any two positive numbers. Calculate the arithmetic and geometric means. Repeat the calculations to generate a sequence of arithmetic means and geometric means. Make a note of what happens to the two sequences.

