Skip over navigation

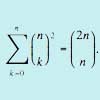
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Summit
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
This neat solution came from Marcos and the result was also
proved by Yatir Halevi:
By the binomial expansion:
$$(1+x)^m=\sum_{t=0}^m \frac{m!}{t!(m-t)!}x^t $$
This can be proved by induction on $m$ but I won't clutter
this with unnecessary proofs.
Putting in $x= -1$ we have
$$0=\sum_{t=0}^m \frac{m!}{t!(m-t)!}(-1)^t
$$
Dividing through by $m!$ gives us the required
result:
$$\sum_{t=0}^m \frac{(-1)^t}{t!(m-t)!}=0 $$
You may also like
Telescoping Series
Find $S_r = 1^r + 2^r + 3^r + ... + n^r$ where r is any fixed positive integer in terms of $S_1, S_2, ... S_{r-1}$.
Binomial
By considering powers of (1+x), show that the sum of the squares of the binomial coefficients from 0 to n is 2nCn

