Skip over navigation

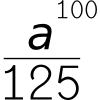
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Binomial
Age 16 to 18
Challenge Level 





Show that
\[\sum_{k=0}^n {n\choose k}^2 \equiv {2n \choose n}.\]
You may also like
Telescoping Series
Find $S_r = 1^r + 2^r + 3^r + ... + n^r$ where r is any fixed positive integer in terms of $S_1, S_2, ... S_{r-1}$.
Remainder Hunt
What are the possible remainders when the 100-th power of an integer is divided by 125?

