Skip over navigation
Why do this problem?
The problem gives practice in using the notation for Binomial coefficients and manipulating algebraic expressions. In problem solving mode, if they can't get started, they might first try to work on the formula for small integer values of $n$.
Possible approach
Use as a revision exercise.
Key questions
If ${2n \choose n}$ is a binomial coefficient in the expansion of some power of $(1 + x)$ what can you say about the expansion and about the term where it occurs?
What do we know about ${n\choose r}$ and ${n\choose n-r}$?
You could ask students to show that the sum of the $n$th row in Pascal's Triangle is $2^n$ first - so that they have a sense of achievement even if they don't succeed in proving the result in this problem.

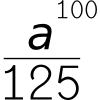
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Binomial
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
The problem gives practice in using the notation for Binomial coefficients and manipulating algebraic expressions. In problem solving mode, if they can't get started, they might first try to work on the formula for small integer values of $n$.
Possible approach
Use as a revision exercise.
Key questions
If ${2n \choose n}$ is a binomial coefficient in the expansion of some power of $(1 + x)$ what can you say about the expansion and about the term where it occurs?
What do we know about ${n\choose r}$ and ${n\choose n-r}$?
Possible support
Ask learners to find the coefficient of $x^2$ in the expansion
of $(1+x)^4$, the coefficient of $x^3$ in the expansion of $(1
+x)^6$ and then the coefficient of $x^4$ in the expansion of $(1 +
x)^8$ and then ask them to try to connect their results to the
problem given.
It might help to do the problem
Summit first.
You could ask students to show that the sum of the $n$th row in Pascal's Triangle is $2^n$ first - so that they have a sense of achievement even if they don't succeed in proving the result in this problem.
You may also like
Telescoping Series
Find $S_r = 1^r + 2^r + 3^r + ... + n^r$ where r is any fixed positive integer in terms of $S_1, S_2, ... S_{r-1}$.
Remainder Hunt
What are the possible remainders when the 100-th power of an integer is divided by 125?

