Skip over navigation
Well done Ang Zhi Ping from River Valley High School, Singapore for your excellent solution to this question.
Let the binomial coefficient $n!/r!(n-r)!$ be denoted by \begin{equation}{n\choose r}.\end{equation}
By considering powers of $(1 + x)$ show that \[\sum_{k=0}^n {n\choose k}^2 = {2n \choose n}\]
As $(1 + x)^n(1 + x)^n = (1 + x)^{2n} \quad (1) $, we write down the Binomial expansion giving: \begin{equation*}\left[\sum_{p=0}^n {n\choose p} x^p\right]\left[\sum_{q=0}^n {n\choose q} x^q\right] = \sum_{r=0}^{2n} {2n\choose r}x^r. \end{equation*} The left hand side of the equation is \begin{equation*}\left[{n\choose 0} + {n\choose 1}x + \cdots + {n\choose n}x^n\right] \left[{n\choose 0} + {n\choose 1}x + \cdots + {n\choose n}x^n\right].\end{equation*} So the coefficient of $x^n$ on the left hand side of (1) is \begin{equation*}{n\choose 0}{n\choose n} + {n\choose 1}{n\choose n-1} + {n\choose 2}{n\choose n-2} + \cdots +{n\choose n-1}{n\choose 1} + {n\choose n}{n\choose 0}.\end{equation*} Since \begin{equation}{n\choose r} = {n\choose n-r}\end{equation} we see that the coefficient of $x^n$ on the left hand side of (1) is \begin{equation}\sum_{k=0}^n {n\choose k}^2.\end{equation} As the coefficient of $x^n$ on the right hand side of (1) is \begin{equation}{2n\choose n}\end{equation} the given formula is proven.

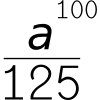
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Binomial
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done Ang Zhi Ping from River Valley High School, Singapore for your excellent solution to this question.
Let the binomial coefficient $n!/r!(n-r)!$ be denoted by \begin{equation}{n\choose r}.\end{equation}
By considering powers of $(1 + x)$ show that \[\sum_{k=0}^n {n\choose k}^2 = {2n \choose n}\]
As $(1 + x)^n(1 + x)^n = (1 + x)^{2n} \quad (1) $, we write down the Binomial expansion giving: \begin{equation*}\left[\sum_{p=0}^n {n\choose p} x^p\right]\left[\sum_{q=0}^n {n\choose q} x^q\right] = \sum_{r=0}^{2n} {2n\choose r}x^r. \end{equation*} The left hand side of the equation is \begin{equation*}\left[{n\choose 0} + {n\choose 1}x + \cdots + {n\choose n}x^n\right] \left[{n\choose 0} + {n\choose 1}x + \cdots + {n\choose n}x^n\right].\end{equation*} So the coefficient of $x^n$ on the left hand side of (1) is \begin{equation*}{n\choose 0}{n\choose n} + {n\choose 1}{n\choose n-1} + {n\choose 2}{n\choose n-2} + \cdots +{n\choose n-1}{n\choose 1} + {n\choose n}{n\choose 0}.\end{equation*} Since \begin{equation}{n\choose r} = {n\choose n-r}\end{equation} we see that the coefficient of $x^n$ on the left hand side of (1) is \begin{equation}\sum_{k=0}^n {n\choose k}^2.\end{equation} As the coefficient of $x^n$ on the right hand side of (1) is \begin{equation}{2n\choose n}\end{equation} the given formula is proven.
You may also like
Telescoping Series
Find $S_r = 1^r + 2^r + 3^r + ... + n^r$ where r is any fixed positive integer in terms of $S_1, S_2, ... S_{r-1}$.
Remainder Hunt
What are the possible remainders when the 100-th power of an integer is divided by 125?

