Skip over navigation
Article by Toni Beardon
We shall explore the similarities between the harmonic triangle, which you see below, and Pascal's triangle. You may like to start by trying this Harmonic Triangle problem.

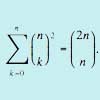
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Age 16 to 18
Published 2006 Revised 2008
The Harmonic Triangle and Pascal's Triangle
We shall explore the similarities between the harmonic triangle, which you see below, and Pascal's triangle. You may like to start by trying this Harmonic Triangle problem.
|
The rule for generating the harmonic triangle is that you add
two consecutive entries to give the entry between them in the row
above. Equivalently, from any term, to get the next term, subtract
that term from the corresponding term on the row above. It is still
possible to work downwards row by row because the entry at the left
hand end of the $n$th row is ${1\over n}$.
For example the third row of the harmonic triangle is:
$${1\over 3},\ {1\over 6},\ {1\over 3}$$ and the fourth row is:
$${1\over 4},\ {1\over 12},\ {1\over 12}, \ {1\over 4}$$ which is
given by $${1\over 4},\ \ \left[{1\over 3}-{1\over 4}\right] ,\ \
\left[{1\over 6}-{1\over 12}\right],\ \ \left[{1\over 3}-{1\over
12}\right]$$
|
\begin{array}{ccccccccccc} & & & & & \frac{1}{1} & & & & & \\ & & & & \frac{1}{2} & & \frac{1}{2} & & & & \\ & & & \frac{1}{3} & & \frac{1}{6} & & \frac{1}{3} & & & \\ & & \frac{1}{4} & & \frac{1}{12} & & \frac{1}{12} & & \frac{1}{4} & & \\ & \frac{1}{5} & & \frac{1}{20} & & \frac{1}{30} & & \frac{1}{20} & & \frac{1}{5} & \\ \frac{1}{6} & & \frac{1}{30} & & \frac{1}{60} & & \frac{1}{60} & & \frac{1}{30} & & \frac{1}{6} \\ & & & & & ... & & & & & \end{array} |
So is it possible to continue generating the harmonic triangle
indefinitely using this rule and will all the terms be fractions
with unit numerators?
| The entries in the harmonic triangle are related by a similar rule to the entries in Pascal's triangle and both sets of entries involve the binomial coefficients. We denote the $r$th entry in the $n$th row of Pascal triangle by the binomial coefficient: $${n-1\choose r-1}= {(n-1)!\over (r-1)!(n-r)!}.$$ For example the sixth row is $${5 \choose 0} = 1 , {5 \choose 1}= 5, {5\choose 2}=10, {5\choose 3}= 10, {5\choose 4}= 5, {5\choose 5} =1 $$ | \begin{array}{ccccccccccc} & & & & & 1 & & & & & \\ & & & & 1& & 1 & & & & \\ & & & 1 & & 2 & & 1 & & & \\ & & 1 & & 3 & & 3 & & 1 & & \\ & 1& & 4 & & 6 & & 4 & & 1 & \\ 1& & 5& & 10 & & 10 & & 5 & & 1 \\ & & & & & ... & & & & & \end{array} |
The rule for generating Pascal's triangle is that you add two
consecutive entries to give the entry between them in the row
below. This rule is given by $${n-1\choose r-1} + {n-1 \choose r} =
{n\choose r}.$$ This is a well known result, it can be proved by
simple algebra and the proof is given in many textbooks.
For the harmonic triangle the $r$th entry in the $n$th row is
given by: $$H(n, r) = {(r-1)!\over n(n-1)(n-2)...(n-r+1)}=
{(r-1)!(n-r)!\over n!}= {1\over n{n-1\choose r-1}}$$ Knowing that
the binomial coefficient ${n-1\choose r-1}$ is a whole number it is
clear from this formula that all the fractions in the harmonic
triangle will have $1$ as numerator.
It remains to prove that the rule for generating the harmonic
triangle works in general for all $n$ and $r$ and then we shall
have established that the harmonic triangle can be extended to $n$
rows for any $n$ by using the given formula for the $r$th entry in
the $n$th row.
The harmonic triangle rule is given by the formula: $$H(n, r)
+ H(n, r+1) = H(n-1, r)$$ or equivalently, as described above,
$$H(n, r+1) = H(n-1, r)-H(n, r).$$ The proof is left to the reader.
All you need to do is substitute the formulae in terms of the
factorials into the right hand side of this identity and simplify
it to get the left hand side. If you want to check that you have
managed to do it correctly you can click on Solution above.
Related Collections
You may also like
Telescoping Series
Find $S_r = 1^r + 2^r + 3^r + ... + n^r$ where r is any fixed positive integer in terms of $S_1, S_2, ... S_{r-1}$.
Binomial
By considering powers of (1+x), show that the sum of the squares of the binomial coefficients from 0 to n is 2nCn

