Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Semi-regular Tessellations



Semi-regular Tesselations printable sheet
Printable sheets - copies of polygons with various numbers of sides 3 4 5 6 8 9 10 12
Regular tessellations use identical regular polygons to fill the plane. The polygons must line up vertex to vertex, edge to edge, leaving no gaps.
Can you convince yourself that there are only three regular tessellations?
- They are formed by two or more types of regular polygon, each with the same side length
- Each vertex has the same pattern of polygons around it.
Explore semi-regular tessellations using the Tessellation Interactivity below.
If you've never used the interactivity before, there are some instructions and a video.
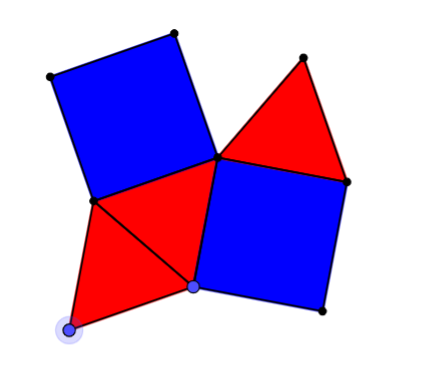
The picture shows an arrangement of equilateral triangles and squares. It looks like there's room for another triangle to fill the gap at the top... but can you prove it will fit?
If we tiled the plane with this pattern, we can represent the tiling as {3, 4, 3, 3, 4}, because round every point, the pattern "triangle, square, triangle, triangle, square" is followed. What would the pattern look like if you changed this order?
Can you find all the semi-regular tessellations?
Can you show that you have found them all?
To help you when you are working away from the computer, click below for multiple copies of the different polygons. You can print them, cut them out and use them to test which polygons fit together: 3 4 5 6 8 9 10 12
You may also like
Triominoes
A triomino is a flat L shape made from 3 square tiles. A chess board is marked into squares the same size as the tiles and just one square, anywhere on the board, is coloured red. Can you cover the board with trionimoes so that only the square is exposed?
LOGO Challenge 5 - Patch
Using LOGO, can you construct elegant procedures that will draw this family of 'floor coverings'?
LOGO Challenge - Triangles-squares-stars
Can you recreate these designs? What are the basic units? What movement is required between each unit? Some elegant use of procedures will help - variables not essential.

