Semi-regular Tessellations

Age 11 to 16

Challenge Level Yellow star

Why do this problem?

Tessellations are a fascinating topic that students of all ages find intriguing. The real world applications of tiling and the opportunity for creating beautiful patterns provide a hook to engage students and stimulate their curiosity, while the interactive environment allows them to quickly test out ideas and make conjectures.

Finding all the possible tessellations provides a context for students to practise working out interior angles of polygons and angles around a point.

Possible approach

Introduce the interactivity to the class, and ask them to consider which shapes you might choose if you wanted to tile an area (with just one type of shape) without leaving any gaps or overlaps.

For each suggestion, use the interactivity to determine whether it does or doesn't tessellate.

Ask the class to think about why some shapes tessellate but others do not. If the class have only suggested triangles, squares or hexagons so far, ask them to speculate on what would happen with pentagons.

Click on the hint for some methods for calculating interior angles of regular polygons, if your students haven't met this before.

Once it is established that the interior angle needs to be a factor of $360^{\circ}$, challenge the class to construct a convincing argument that there are only three regular tessellations.

Next, introduce the concept of semi-regular tessellations:

"What if you were allowed to use more than one type of shape to tile your area?"

Ask the students for suggestions or show them this image:

"What shape would I need to fill the gap at the top? Will it fit exactly? How do you know?"
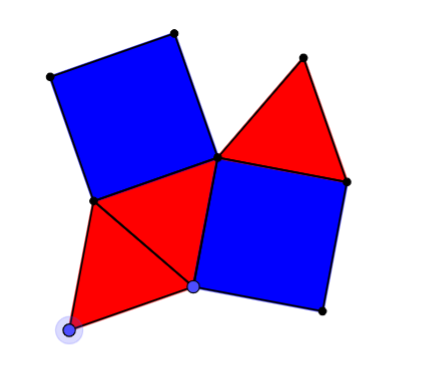
Three equilateral triangles plus two squares gives 60+60+60+90+90=360$^{\circ}$.

Then introduce the notation describing the polygons around each vertex - {3, 4, 3, 3, 4} for the example above.

NB in a semi-regular tessellation, each vertex must have exactly the same shapes in exactly the same order (but can be clockwise or anticlockwise). For example, with triangles and hexagons, if you put {3, 6, 6, 3} round one point, you can't have {3, 6, 3, 6} round another.

Set students the challenge of finding semi-regular tessellations.

Encourage students to use the interior angles to calculate combinations of shapes which might tessellate. Once they have made a prediction, they can test it using the interactivity or shapes printed off and cut out. (here are some 3, 4, 5, 6, 8, 9, 10, 12 sided regular polygons to print.)

It is very important that students try sufficient shapes to verify that the tessellation will work - a decagon and two pentagons, for example, will fit together around a point but the pattern cannot be continued.

Once students have had a chance to find one or two semi-regular tessellations, challenge them to find them all, and to provide convincing evidence that they have got the complete set.

Key questions

Why do some shapes fit together and others don't?

Can you tell in advance whether shapes will tessellate, without using the interactivity?

Can you organise your work in such a way as to convince someone you have found all the semi-regular tessellations?

Possible support

Students could begin by exploring tessellation of quadrilaterals, paying particular attention to the angle properties.

Possible extension

Can students explain why some patterns work around a point but don't tile the area? For example, the decagons and pentagons suggested above. Challenge students to find other similar examples (which could use polygons with more than 12 sides, such as {18, 9, 3}).

Suggest students read Shaping up with Tessellations.

Move on to three dimensions: Which Solids Can We Make?

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Semi-regular Tessellations

Why do this problem?

Possible approach

Key questions

Possible support

Possible extension

You may also like

Triominoes

LOGO Challenge 5 - Patch

LOGO Challenge - Triangles-squares-stars