Squares in Rectangles

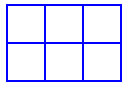
A $2$ by $3$ rectangle contains $8$ squares:

six small $1\times 1$ squares and two larger $2 \times 2$ squares



A $3$ by $4$ rectangle contains $20$ squares:

twelve $1\times1$ squares, six $2 \times 2$ squares and two $3 \times 3$ squares

Consider rectangles with a height of $2$ units.
Increase their width by $1$ unit at a time.
What effect does this have on the total number of squares?

Make a note of the number of squares in rectangles with a height of $2$ units.
Do you notice anything special?

Use your results to decide whether a rectangle with a height of $2$ units can contain exactly $100$ squares?

What about rectangles with a height of $3, 4, 5, \ldots$?

Draw up a table of results.