Skip over navigation
Whirling Fibonacci Squares
 |
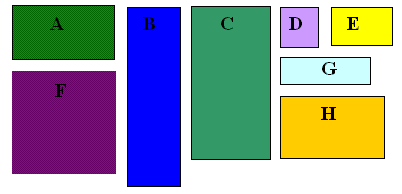Which of these rectangles are the same shape? Can you find
pairs of the same shape?
How can you be sure that they are exactly the same shape and
not just nearly the same shape? The colours give a clue but there
is a mathematical property here that you can use to test if two
rectangles are the same shape.
Can you work out what that property is?
|
Two rectangles are the same shape if one is an enlargement of
the other. You can test them by finding the ratio of the length of
the long side divided by the length of the short side.
For example F and D are squares and the shape ratio is
1.
The long thin rectangles B and G have shape ratio 3.5 and
rectangles A and C have shape ratio 2.
Rectangles E and H are golden rectangles and they have a shape
ratio which is called the golden ratio, for which the symbol $\phi$
is often used. We are going to find out more about $\phi$.
The Fibonacci sequence 1, 1, 2, 3, 5, 8,13, 21, 34, 55, ... is
defined by the rule that you start with the first two terms 1, 1
and add two successive terms in the sequence to get the next term.
The rule for this sequence can be written as a formula with $F_n$
for the $n^{th}$ Fibonacci number: $F_n = F_{n-1}+ F_{n-2}$, with
the first two terms: $F_1=1, F_2=1.$
What does the Fibonacci sequence have to do with golden
rectangles and the golden ratio? The following activity shows the
connections.
Find a piece of squared paper or download one here.
 |
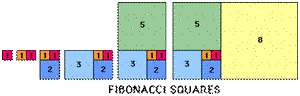As in this diagram, draw two squares of unit area side by side
on your squared paper, then a square of side 2 units to make a 3 by
2 rectangle, then a square of side 3 units to make a 5 by 3
rectangle, and continue drawing squares whose sides are given by
the Fibonacci numbers until you fill your piece of paper.
|
We call these 'whirling squares' because they spiral round and
round. Try to draw as many squares as you can on your sheet of
paper by carefully positioning the first two squares. Now imagine
that the paper extends for ever in all directions and the process
continues indefinitely. What happens to the shapes of the
rectangles?
Look at the rectangles in your 'whirling squares' diagram: 1
by 1, 2 by 1, 3 by 2, 5 by 3, 8 by 5 ... and so on. You will see
that the ratios of the long side to the short side of the
rectangles, given by the ratio of successive Fibonacci numbers,
starts off as $${1\over 1}=1, {2\over 1}=2, {3\over 2}=1.5, {5\over
3} = 1.666.., {8\over 5}=1.6,....\mbox{ and so on}$$ Now use a
calculator and work out the next ten ratios. What do you
notice?
Now you can experiment using a spreadsheet. This will be handy
if you don't have a calculator, and if you have worked the ratios
out for yourself the spreadsheet will enable you to discover
more.
 |
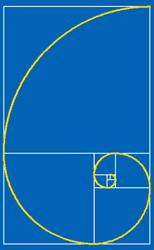OK, if you have explored the ratios using the spreadsheet you
have some pretty convincing evidence that the ratio of successive
terms of the Fibonacci sequence tends to the limit called the
golden ratio which has a value $\phi \approx 1.618$.This is a fact
but we have not proved it yet.
Now you might like to draw this spiral for yourself on the
whirling squares diagram you have already drawn. Just draw the
curve from corner to corner across each square.
|
You may also like
Marbles
I start with a red, a green and a blue marble. I can trade any of my marbles for two others, one of each colour. Can I end up with five more blue marbles than red after a number of such trades?
More Marbles
I start with a red, a blue, a green and a yellow marble. I can trade any of my marbles for three others, one of each colour. Can I end up with exactly two marbles of each colour?
Rolling Triangle
The triangle ABC is equilateral. The arc AB has centre C, the arc BC has centre A and the arc CA has centre B. Explain how and why this shape can roll along between two parallel tracks.