Skip over navigation
I have decided to make another patchwork quilt. The end result should look something like this:
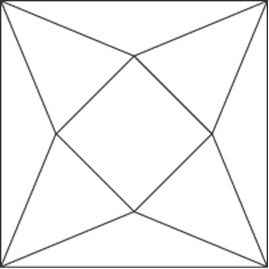
It is a design known as "World without end" and is based on a series of squares like this:
A Patchwork Piece
Age 7 to 11
Challenge Level 
A PAtchwork Piece
I have decided to make another patchwork quilt. The end result should look something like this:
It is a design known as "World without end" and is based on a series of squares like this:
The problem is to make the individual pattern pieces the right size (and shape!).
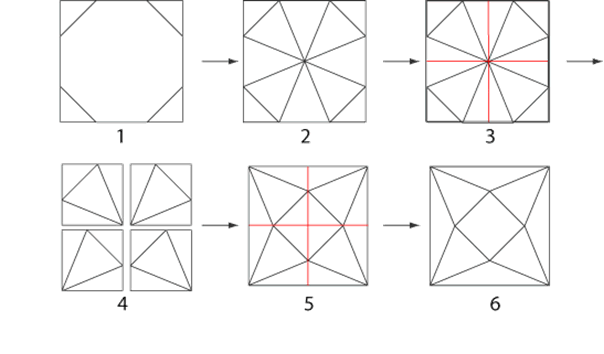
Although it is not exactly obvious this design is based on a regular octagon in a square. These diagrams show the transformations required:
This helps in making the individual pattern pieces. Can you work out how each of the above steps was achieved? Try it with a square piece of paper.
How could you make the pattern if you only have a ruler and a pair of scissors?
What about if you were allowed to use a pair of compasses as well?
Let us know how you achieved each step. You can send in pictures of your final piece, too.
_________________________
Here are the first four squares of the actual quilt:
Why do this problem?
This problem encourages learners to develop their spatial reasoning. The fact that they are asked to recreate the pattern pieces gives them the opportunity to do amathematical construction which is perhaps quite rare at this level.
Possible approach
A nice way to start this activity might be to put up a picture of final design and then of a single square.
Invite the group to talk about what they can see. (Children will often call this a diamond which gives a good opportunity to discuss the properties of a square.)
When the class begin to work on the problem itself, encourage them to work in pairs. Their conversations will help you to assess their knowledge and understanding of properties of 2D shapes, and how readily they use vocabulary associated with shape and position.
By far, the easiest way to do this construction is to start with an octagon and draw the square round it. Drawing an accurate regular octagon in a set sized square requires mathematical knowledge beyond primary level. Otherwise children can make a design in which the octagon is not regular.
By far, the easiest way to do this construction is to start with an octagon and draw the square round it. Drawing an accurate regular octagon in a set sized square requires mathematical knowledge beyond primary level. Otherwise children can make a design in which the octagon is not regular.
Key questions
What you can see in this design?
What different shapes are there in the picture? Tell me about them.
Which shapes are the same and which are different?
What can you tell me about the shape in the middle?
How are you going to draw regular octagon?
What size are the eight internal angles?
