Skip over navigation
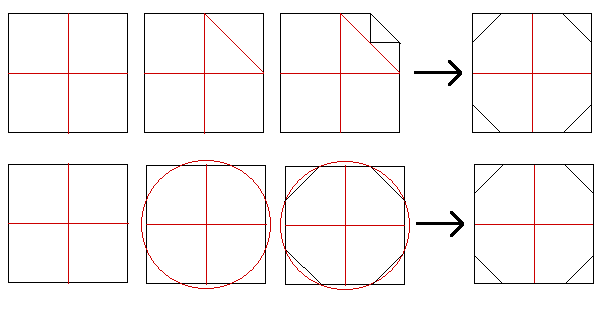
An alternative method is to use a compass. Note that all of the vertices of the octagon are an equal distance from the centre, so if you draw a circle and mark the intersections with the square, this will give you 8 vertices.
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
A Patchwork Piece
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Step 1
The octagon doesn't need to be regular, so the triangles in the four corners of the square can be any size as long as they are all the same. So, you could start by folding the square into quarters to find the centre, then fold in each of the corners. This would give you a square inside a square, so you need to fold in each corner a second time, up to the first set of folds.An alternative method is to use a compass. Note that all of the vertices of the octagon are an equal distance from the centre, so if you draw a circle and mark the intersections with the square, this will give you 8 vertices.

Step 2
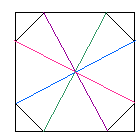
The second stage of the pattern is formed by joining together diagonally opposite pairs of vertices.
Step 3
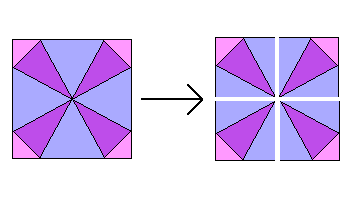
Now you can cut the square into four smaller squares using the fold lines that you already have from Step 1. At this point it is easier to see what is going on if you colour in the pieces.
Steps 4,5 and 6
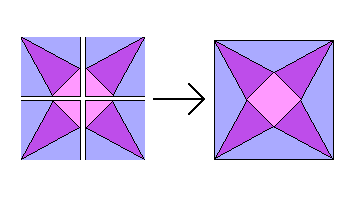
Now that the areas are coloured, can you see that each section has to be rotated individually by 180 °? When you stick the four pieces back together again you are left with the finished pattern!
Try it for youself with your own colour scheme, and see if you can find any different ways of making the pattern. You could even come up with a pattern of your own using the same methods!

