Skip over navigation
Firstly an obvious chunk would be the trace for one revolution of the wheel because that's clearly going to repeat (the period).
You might notice that the first half and the second half of the period match each other in a particular way - how would you describe that kind of mathematical matching and, most importantly, can you account for it?
Symmetric Trace
Age 14 to 16
Challenge Level 
This is a Three Star Challenge so you won't be expecting a quick fix.
But as a hint : split the trace into chunks that mean something.Firstly an obvious chunk would be the trace for one revolution of the wheel because that's clearly going to repeat (the period).
You might notice that the first half and the second half of the period match each other in a particular way - how would you describe that kind of mathematical matching and, most importantly, can you account for it?
All three traces have this property but the "same when upside-down" quality isn't there for all of them.
What makes that "same when upside-down" work?You may also like
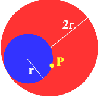
Just Rolling Round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
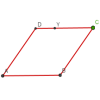
Roaming Rhombus
We have four rods of equal lengths hinged at their endpoints to form a rhombus ABCD. Keeping AB fixed we allow CD to take all possible positions in the plane. What is the locus (or path) of the point D?
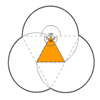
Triangles and Petals
An equilateral triangle rotates around regular polygons and produces an outline like a flower. What are the perimeters of the different flowers?