Maximum Scattering

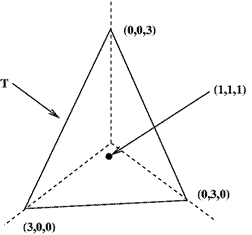
a) The data obtained from a given experiment is a pair of numbers $a$ and $b$, where $a\geq 0$ and $b\geq 0$. It is known that $a$ and $b$ have mean $1$; what is the largest value that the standard deviation can be? (b) The data obtained from a given experiment is a triple of numbers $x$, $y$ and $z$, where each is non-negative. It is known that the mean of $x$, $y$ and $z$ is $1$; what is the largest value that the standard deviation can be?

(c) The data obtained from a given experiment is a set of numbers $t_1,\ldots,t_n$, where each is non-negative. It is known that the mean of the $t_j$ is $1$. Show that the standard deviation may be as large as $\sqrt{n-1}$.