Skip over navigation
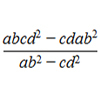
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
There's Always One Isn't There
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Systematic working and recording of results help a lot here.
Conjectures are important, and should be encouraged, but along with a challenge to really explain why any claim might be true generally.
We are so familiar with numbers and what they do, or what we believe they do, that the challenge to account rigorously for the familiar can seem pedantic. Hopefully the problem expressed in this form will give students the pleasure of discerning real structure.
You may also like
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.

