Mirror, Mirror...
Mirror, Mirror... printable sheet
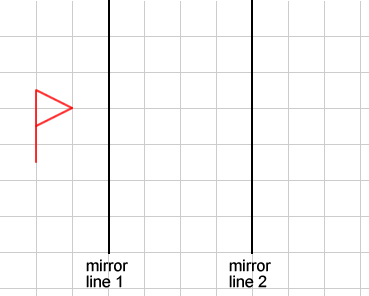
You might like to copy the diagram above onto squared paper to help you with this problem.
Reflect the flag in the left-hand line, and then reflect the image you obtain in the right-hand line.
Can you describe the single transformation that takes the first flag to the last flag?
Repeat this with flags in different positions and orientations, and with different pairs of parallel lines.
Does it matter in which line you reflect first?
Does it matter whether the flag is to one side of the lines or between the lines?
Can you describe the single transformation that takes the first flag to the last flag for any pair of parallel lines?
If you have enjoyed this problem, why not have a go at ...on the Wall and Who is the fairest of them all? ?
You may also like
Frieze Patterns in Cast Iron
A gallery of beautiful photos of cast ironwork friezes in Australia with a mathematical discussion of the classification of frieze patterns.
The Frieze Tree
Patterns that repeat in a line are strangely interesting. How many types are there and how do you tell one type from another?
Friezes
Some local pupils lost a geometric opportunity recently as they surveyed the cars in the car park. Did you know that car tyres, and the wheels that they on, are a rich source of geometry?