Skip over navigation
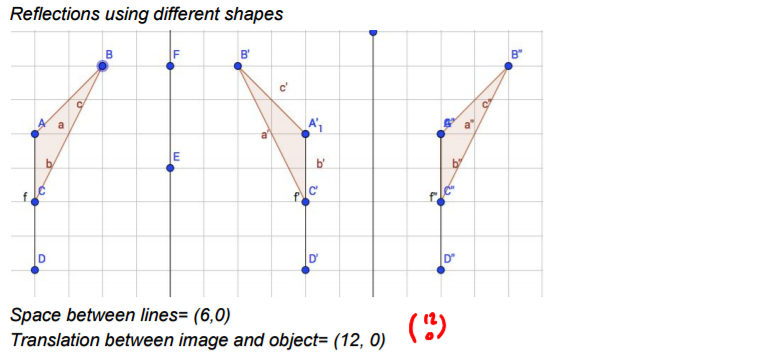
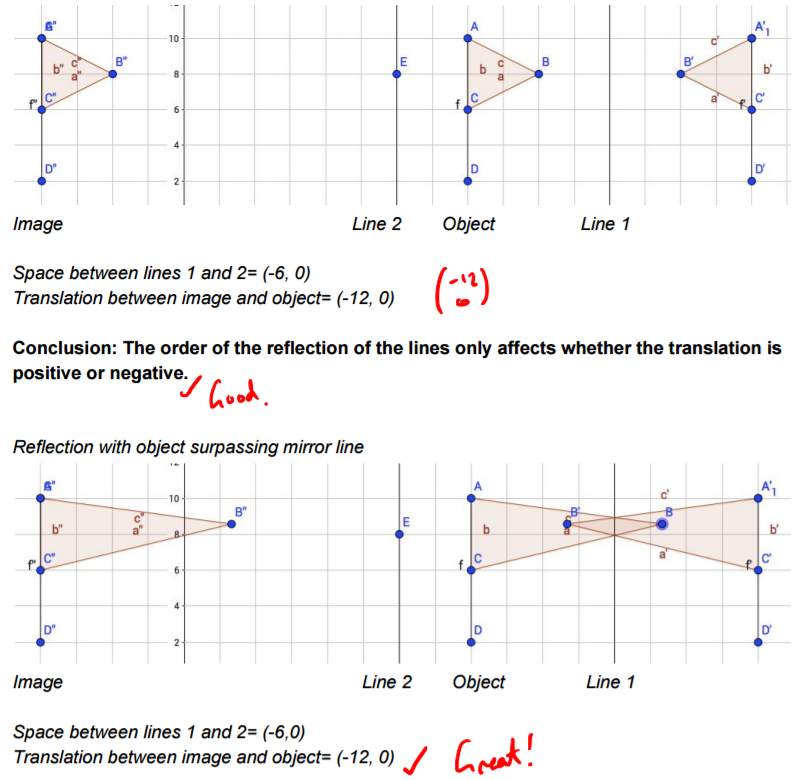
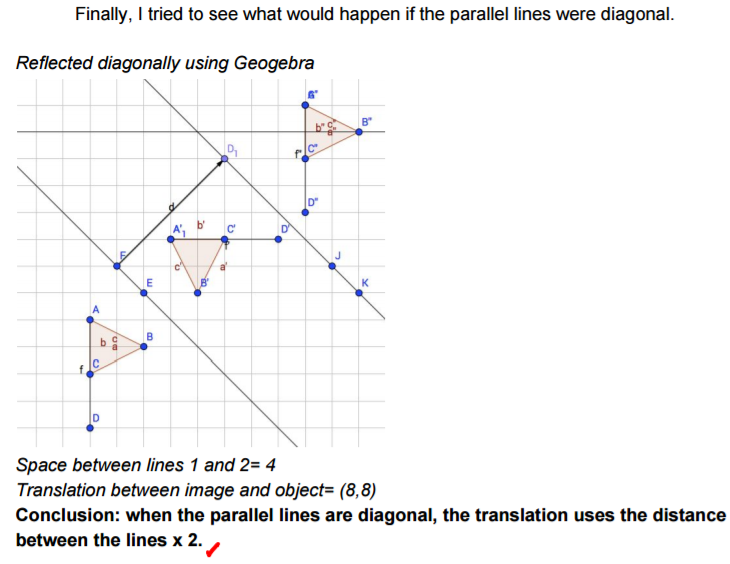
Isabel went on to investigate what happens for different shapes, and if the shape is reflected in the other mirror line first.
Mirror, Mirror...
Age 11 to 14
Challenge Level 
Isabel from St Andrew's Scots School in Argentina used Geogebra to investigate the problem. This is Isabel's work, with some teacher comments.
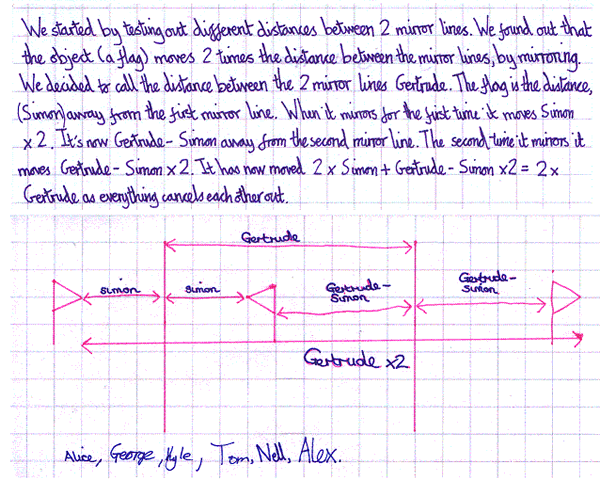
Alice, George, Kyle, Tom, Nell and Alex from Gorseland Primary School explained why this happens:
Isabel went on to investigate what happens for different shapes, and if the shape is reflected in the other mirror line first.
You may also like
Frieze Patterns in Cast Iron
A gallery of beautiful photos of cast ironwork friezes in Australia with a mathematical discussion of the classification of frieze patterns.
The Frieze Tree
Patterns that repeat in a line are strangely interesting. How many types are there and how do you tell one type from another?
Friezes
Some local pupils lost a geometric opportunity recently as they surveyed the cars in the car park. Did you know that car tyres, and the wheels that they on, are a rich source of geometry?