Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Square Tangram



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Square Tangram
A set of shapes has five pieces:
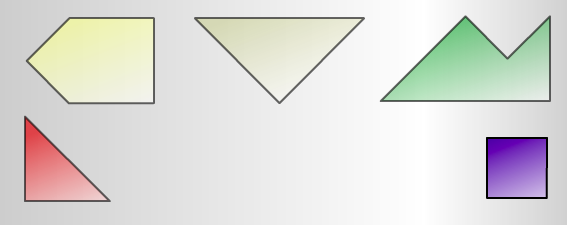
Can you make a square using four of the pieces?
You may like to use the interactivity below to try out your ideas, or download this sheet with two sets of pieces for printing and cutting.
Now, can you make a square using all five pieces?
Now, add another set of five pieces (so now there are ten). Can you make a square with all of them?
Printable NRICH Roadshow resource.
Why do this problem?
This tangram is a challenging context in which to remind pupils of the properties of squares. Tangrams offer a fantastic starting point for nurturing flexibility in the primary classroom. To find out more about developing mathematical flexibility through geometry, take a look at this article.
Possible approach
You could display the interactivity on the board and start by asking children to look at the image on the left (of the tangram pieces). Invite them to consider what they see and what they might like to ask. Give them time to think on their own, then talk to a partner about their 'noticings'. Encourage some pairs to share their observations and questions with the whole group. Try to take a step back and allow the class to respond to the comments and questions themselves, rather than you validating all contributions. Some children might talk about the different shapes they can see (and colours). Encourage use of mathematical vocabulary where appropriate. Build on their thoughts to introduce the idea of a tangram and the task itself.
You can then set the class off in pairs on the challenges. After some time, invite them to offer 'hints' for the rest of the group, without giving away a solution. Perhaps they can offer advice about what they are finding helpful to focus on as they tackle the challenges, perhaps they can suggest a starting point for one of the squares... It is important that children become more confident at simply 'having a go' and playing with their ideas to begin with, rather than feeling that they need to know the 'right' way to do it from the start. You might like to model this trial and improvement approach, emphasising that we can learn a lot from what doesn't work.
These challenges are not straightforward and learners are likely to get stuck. Talk about this with the class. How does it feel to be stuck? How are they trying to get unstuck? How does it feel when they make a breakthrough? You can stop the class as appropriate to share experiences.
The completed squares could make a lovely classroom display, accompanied by some brief notes written by the class, focusing on how they went about finding solutions.
Key questions
What have you tried so far?
Is there a way to tweak what you have done, rather than starting from scratch again?
How will you remember what you have tried?
Possible extension
Learners could create 'clue cards' to offer support to their peers, without giving away the solution.
Possible support
Encouraging a playful approach to this task will help make it accessible to all learners.
You may also like
Cutting Corners
Can you make the most extraordinary, the most amazing, the most unusual patterns/designs from these triangles which are made in a special way?
Cut and Make
Cut a square of paper into three pieces as shown. Now,can you use the 3 pieces to make a large triangle, a parallelogram and the square again?
Square to L
Find a way to cut a 4 by 4 square into only two pieces, then rejoin the two pieces to make an L shape 6 units high.

