Street Sequences
Street Sequences
What do you notice about these two front doors?
Where I live, the houses in many streets are numbered like this, so that the odd numbers are on one side of the road, and the even numbers on the other.
Here is a picture of one side of an imaginary street, with the houses numbered in that way:
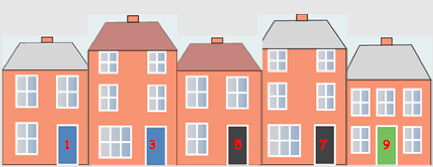
Viewed from above, the house numbers along the street could look like this:
Imagine walking down this street and adding the house numbers in various ways...
You could start with adding in pairs across the street like this:
Have a go.
What do you notice about the answers to your addition calculations?
Can you explain why these patterns occur?
You could change the grouping of houses in different ways. How about:
What happens now?
Can you explain any patterns you notice?
Perhaps the houses are already grouped in some way, for example they may all be semi-detached:
You could add houses that are joined, so on one side of the street the totals are 4, 12, 20... and the other side are 6, 14, 22...
You could continue this and explore it further.
You will have your own ideas about what to explore. For inspiration, why not take a walk down a street near you?
Let us know what you investigate, whether it is one of the suggestions above, or something you have come up with yourself.
We would love to hear about the patterns you see, and your explanations for why those patterns occur.
Why do this problem?
This problem offers opportunities for pupils to explore number patterns in their own way. As well as applying number and calculation skills, learners will have the chance to make conjectures and reason mathematically as they try to explain the patterns they observe.
Possible approach
This problem featured in the NRICH Primary webinar in April 2022.
Ideally, you could introduce this task by taking your class on a short walk to observe house numbering in nearby streets. While many residential roads are numbered with odds on one side and evens on the other, this is not always the case so you may wish to check what your neighbouring streets are like beforehand. Ask learners what they notice about the numbering as you walk.
You can then facilitate a discussion about the children's observations and introduce the idea of representing the house numbers in a plan view. You can lead into the first part of the task by suggesting that as you walk down the street, you might add the house numbers in various ways. To give the group a flavour of this, begin with adding diagonal pairs across the street. Set children off in pairs exploring these sums, and then draw them back for a mini plenary. What have they noticed? Some will offer their observations about when the totals are the same, some may mention the totals increasing by the same amount as they move to the next group of four house numbers.
Let the class know that mathematicians like to be sure that a pattern they have observed will always be true. Can the children explain why their noticings will always be true? Give them time in pairs to talk about this and circulate so you can listen in on their discussions. You could warn a few pairs that you'd like them to share their thinking with the whole class in the next mini plenary. Listen out for those who realise that consecutive odd numbers increase by 2, and so do consecutive even numbers. So, when adding diagonally across the street, although you have an odd that is bigger by 2 compared with its next-door odd, it is being added to an even that is less than 2 compared with its next-door even.
At this point, you can invite learners to consider an alternative way of adding the house numbers. You could show them some ideas from the problem, or you can encourage them to explore their own ideas. Leave enough time in the final plenary for a few pairs to report back on their investigation and the associated noticings, and explanations.
Key questions
What do you notice about your answers?
Why does that pattern or patterns occur?
What could you explore now?
Possible support
Some pupils may find digit cards useful to represent the house numbers. Calculators could also be helpful to free learners up to think creatively.
Possible extension
If it has not come up naturally, you could introduce the idea that some streets have terraces of three houses together:
and some have fours:
Learners can explore the addition of these groups too!
You may also like
Prompt Cards
These two group activities use mathematical reasoning - one is numerical, one geometric.
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.