Skip over navigation
I think that it's time to look at Pascal's Triangle afresh. So, let's see what happens when we turn it around in a special way.
So we start with the layout as usual, turn it anticlockwise 45 degrees and then take off the top line of ones.
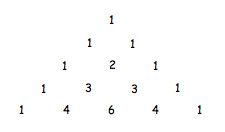
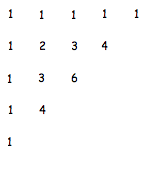

So the first 9 lines would look like this ;
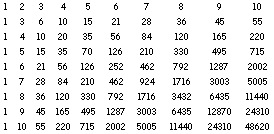

So here you have an awful lot of numbers in rows and columns to explore.
Those of you with some spreadsheet experience (or those of you that are quick to learn such things!) should go to the HINT at this point, before going further.
Some starting points for further explorations.
1. On my spreadsheet I decided to explore the rows that are multiples of 9 as I had noticed that there were a lot of 141's and 171's in those lines. Because that is what I wanted to explore I only wrote down the first number that comes after the patterns I was exploring [that's why there are lots of spaces in two out of every three rows.]

So you could do a similar thing, looking at line numbers of a different multiple.
If you do a few you then could compare your discoveries.
2. You could take just one line [e.g.30] and use the spreadsheet to extend it very far.
Here I've taken line 30, and grouped the numbers in that row in 9's and then three 9's together and underneath each other. I did this because my eyes led me to some interesting repetitions. I then noted down things according to the columns I had placed them under.
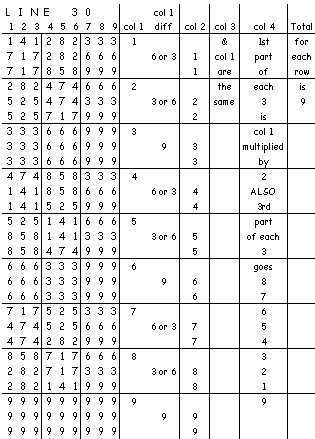
See what other things you can notice with this line or any other that you choose.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Investigating Pascal's Triangle
Age 7 to 11
Challenge Level 





I think that it's time to look at Pascal's Triangle afresh. So, let's see what happens when we turn it around in a special way.
So we start with the layout as usual, turn it anticlockwise 45 degrees and then take off the top line of ones.

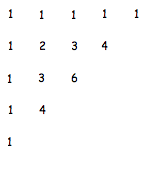

So the first 9 lines would look like this ;

BUT if we take the digital roots of the numbers and see the
first 30 lines we have a new look to Pascal's Triangle as shown
below.

So here you have an awful lot of numbers in rows and columns to explore.
Those of you with some spreadsheet experience (or those of you that are quick to learn such things!) should go to the HINT at this point, before going further.
Some starting points for further explorations.
1. On my spreadsheet I decided to explore the rows that are multiples of 9 as I had noticed that there were a lot of 141's and 171's in those lines. Because that is what I wanted to explore I only wrote down the first number that comes after the patterns I was exploring [that's why there are lots of spaces in two out of every three rows.]

So you could do a similar thing, looking at line numbers of a different multiple.
If you do a few you then could compare your discoveries.
2. You could take just one line [e.g.30] and use the spreadsheet to extend it very far.
Here I've taken line 30, and grouped the numbers in that row in 9's and then three 9's together and underneath each other. I did this because my eyes led me to some interesting repetitions. I then noted down things according to the columns I had placed them under.

See what other things you can notice with this line or any other that you choose.
a) Look for additions that are
interesting;
b) Look at repeats of
numbers;
c) Look for reflections of
patterns.
AND see if you can explainWHY? these patterns are
occurring.
You may also like
The Great Tiling Count
Compare the numbers of particular tiles in one or all of these three designs, inspired by the floor tiles of a church in Cambridge.
Smaller and Smaller
Can you predict, without drawing, what the perimeter of the next shape in this pattern will be if we continue drawing them in the same way?

