Skip over navigation
The solution here uses 3D Cartesian coordinates and the cosine rule. For a similar problem with a solution that uses scalar products of vectors see Air Routes. A third method is to draw an altitude of the isosceles triangle with London, Sydney and the origin as vertices and use the trigonometry of the right-angled triangle.
Flight Path
Age 16 to 18
Challenge Level 
The solution here uses 3D Cartesian coordinates and the cosine rule. For a similar problem with a solution that uses scalar products of vectors see Air Routes. A third method is to draw an altitude of the isosceles triangle with London, Sydney and the origin as vertices and use the trigonometry of the right-angled triangle.
 |
This solution comes from Andrei from Tudor Vianu National College, Bucharest, Romania.
To solve this problem I see that the data are given in spherical coordinates, but I need to work in Cartesian coordinates.
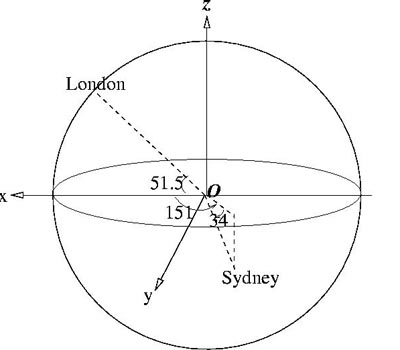
I choose the Cartesian system of coordinates with the origin at the centre of the Earth, with the $xy$ plane - the equatorial plane, and the $z$ axis directed towards the North Pole. The spherical system of coordinates has the origin at the same point as the Cartesian one, i.e. at the centre of the Earth. Let the angle $p$ measure the latitude (0 at the equator and $\pi/2$ at the North
Pole), i.e. it is the angle between the position vector of the current point $P$ and the plane $xOy$. Let the angle $q$ measure the longitude (in respect to the axis $Ox$), i.e. it is the angle between the projection of the position vector of point $P$ on the plane $xOy$ and the $x$ axis. So the 3D coordinates in terms of the angles of latitude and longitude are: $$x = R \cos p \cos q, y = R \cos
p \sin q, z = R \sin p.$$
|
London has longitude 0 and latitude 51.5 degrees North and Sydney has longitude 151 degrees East and latitude 34 degrees South. The corresponding angles for London and Sydney are: $p_L = 51.5, q_L = 0, p_S = -34, q_S = 151$.
The distance between the two cities, measured on the line joining them and passing through the interior of Earth, is: $$d^2 = R^2 ((x_L - x_S)^2 + (y_L - y_S)^2 + (z_L - z_S)^2).$$ Both cities are situated on the sphere, and this means there exists a great circle of the Earth passing through both of them. Let $\alpha$ be the angle between the two cities, and having the vertex at the centre
of the Earth (defined on the great circle specified above). This angle can be found using the cosine rule for the isosceles triangle defined by the position of London, the centre of Earth and the position of Sidney: $$d^2 =R^2 + R^2 - 2R^2 cos \alpha$$ So, $$\cos \alpha = {2R^2 - d^2\over 2R^2}.$$ The distance between the two cities measured on the surface of the Earth, along the great circle, is
$R\alpha$, where $\alpha$ is measured in radians. Let it be $L_1$, then: $$L_1 = R\cos^{-1}{(2 - (x_L-x_S)^2 - (y_L-y_S)^2 - (z_L-z_S)^2) \over 2}.$$ The other distance is calculated adding 6 km to the radius of the Earth, and it will be $L_2$.
The numerical results are: $\alpha = 2.66$ radians and, on the surface of Earth, the distance, to the accuracy of the measures used, is: $$L_1 = 17000 \ {\rm km}.$$ At the altitude of 6 km the distance $L_2$ is about 16 kilometres more than $L_1$.
The results are in reasonable agreement with the distance: 16972 km according to Google Earth and 16997 km on http://portcanal.co.uk/cgi-bin/diser.pl?a=London&b=Sydney
The problem Over the Pole shows that the great circle distance is shorter than the path along a line of latitude for two points with the same latitude.
You may also like
2D-3D
Two circles of equal size intersect and the centre of each circle is on the circumference of the other. What is the area of the intersection? Now imagine that the diagram represents two spheres of equal volume with the centre of each sphere on the surface of the other. What is the volume of intersection?
The Dodecahedron Explained
What is the shortest distance through the middle of a dodecahedron between the centres of two opposite faces?
When the Angles of a Triangle Don't Add up to 180 Degrees
This article outlines the underlying axioms of spherical geometry giving a simple proof that the sum of the angles of a triangle on the surface of a unit sphere is equal to pi plus the area of the triangle.