Skip over navigation
Each black card makes you lose half your money - which is the same as multiplying what you have by 0.5.
Each red card multiplies what you have by 1.5 since you win half of the cash you have.
As there are 3 reds and 3 blacks, the total amount you will finish with will be:
"starting amount" x 0.5 x 0.5 x 0.5 x 1.5 x 1.5 x 1.5 = starting amount x 0.42 (approx).
Since you can multiply in any order, you will always end up with the same amount! ( £54)
As multiplication is commutitive whatever order the cards are placed the results will be the same!
A lose followed by a win results in a return of 3/4 (0.5 x 1.5) of your stake.
This is with a ratio of 1:1 red:black.
Given the 6 cards the return is 27/64 of your stake.
In order to win, the ratio of red:black cards has got to be at least 1.71:1.
This is because in order to cancel the effect of one black card which is multiplying by 0.5 you need to multiply it by at least 2 as 0.5 x 2 = 1.
Since each red card multiplies by 1.5 you need to find the number (power) of 1.5's you need to multiply to get 2.
That is, what is x if $1.5^x$ is going to be greater than or equal to 2? (Answer: x has to be greater than or equal to 1.71)

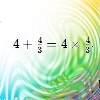
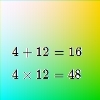
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
A Chance to Win?
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Tim explained clearly why you can never win:
It doesn't matter what order you play the cards!Each black card makes you lose half your money - which is the same as multiplying what you have by 0.5.
Each red card multiplies what you have by 1.5 since you win half of the cash you have.
As there are 3 reds and 3 blacks, the total amount you will finish with will be:
"starting amount" x 0.5 x 0.5 x 0.5 x 1.5 x 1.5 x 1.5 = starting amount x 0.42 (approx).
Since you can multiply in any order, you will always end up with the same amount! ( £54)
Charlie, Gemma, Griselda, Tom, Jason and Greg from Colyton Grammar School also worked out what was happening:
It does not matter in what order the cards are put down because the result of using a win card is that your money is multiplied by 1.5 and the result of you using a lose card is that your money is multiplied by 0.5.As multiplication is commutitive whatever order the cards are placed the results will be the same!
A lose followed by a win results in a return of 3/4 (0.5 x 1.5) of your stake.
This is with a ratio of 1:1 red:black.
Given the 6 cards the return is 27/64 of your stake.
In order to win, the ratio of red:black cards has got to be at least 1.71:1.
This is because in order to cancel the effect of one black card which is multiplying by 0.5 you need to multiply it by at least 2 as 0.5 x 2 = 1.
Since each red card multiplies by 1.5 you need to find the number (power) of 1.5's you need to multiply to get 2.
That is, what is x if $1.5^x$ is going to be greater than or equal to 2? (Answer: x has to be greater than or equal to 1.71)
You may also like
Tweedle Dum and Tweedle Dee
Two brothers were left some money, amounting to an exact number of pounds, to divide between them. DEE undertook the division. "But your heap is larger than mine!" cried DUM...
Sum Equals Product
The sum of the numbers 4 and 1 [1/3] is the same as the product of 4 and 1 [1/3]; that is to say 4 + 1 [1/3] = 4 � 1 [1/3]. What other numbers have the sum equal to the product and can this be so for any whole numbers?
Special Sums and Products
Find some examples of pairs of numbers such that their sum is a factor of their product. eg. 4 + 12 = 16 and 4 × 12 = 48 and 16 is a factor of 48.

