Pythagoras on a Sphere

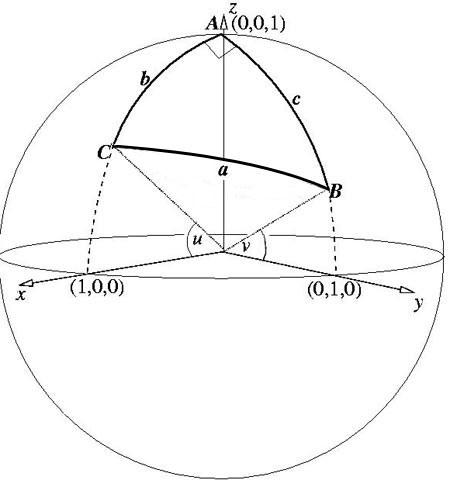
All angles are in radians.

(1) Without loss of generality take coordinate axes so that $A$ is the point$(0,0,1)$, the xz-plane contains the point $C$ and the yz-plane contains the point $B$.

(2) Thinking of $A$ as the North Pole then $C$ has latitude $u$ and longitude 0 and $B$ has latitude $v$ and longitude $\pi/2$.

(3) Find the 3D coordinates of $B$ and $C$. Where the origin O is the centre of the sphere ${\bf OA, OB}$ and ${\bf OC}$ are vectors of unit length.

(4) Use scalar products and vectors ${\bf OA, OB}$ and ${\bf OC}$ to find the lengths of the arcs $AB, BC$ and $CA$ in terms of $u$ and $v$. The required result follows.