Skip over navigation
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Pythagoras on a Sphere
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
 |
Many thanks Andrei from Tudor Vianu
National College, Bucharest, Romania for another excellent
solution.
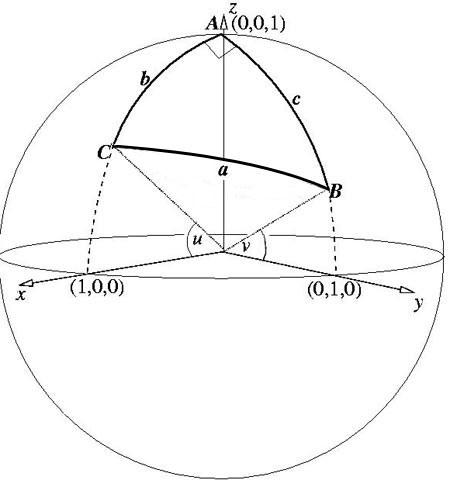
To solve the problem I have used the hint, so that all
notations are from the hint. I have associated to the sphere a
system of Cartesian coordinates, as shown in the sketch.
Without loss of generality, I have assumed that $A$ is
situated on $Oz$, and has coordinates (0, 0, 1). As $A$ is a right
angle, I can assume that $B$ is situated in the plane $yOz$ and $C$
in plane $xOz$ respectively.
Let the angle $xOC$ be $u$, and angle $yOB$ be $v$. So, the
Cartesian coordinates of the three points, which correspond to the
vectors OA, OB and
OC , are: $$A(0, 0, 1),\
B(0, \cos v, \sin v),\ C(\cos u, 0, \sin u).$$
|
Arcs $AB, BC$ and $CA$ are arcs on the three great circles (of
radius unity), so that their lengths are equal to the angles at the
centre in the corresponding great circle (expressed in radians).
So, as shown in the figure: $$\angle BOC = a,\ \angle AOC = b =
{\pi \over 2} - u, \ \angle AOB = c = {\pi \over 2} - v. \quad
(1)$$ To calculate the length of arc $BC$ I use the same procedure
as in the problem "Flight path". I calculate first the straight
line distance between $B$ and $C$ inside the Earth: $$BC^2 = \cos^2
u + \cos^2 v + \sin^2 u + \sin^2 v - 2\sin u \sin v = 2 (1 - \sin u
\sin v). \quad (2)$$ But from (1) I observe that $\sin u = \cos b$
and $\sin v = \cos c$. Using these and (2), I obtain $BC^2$: $$BC^2
= 2 (1 - \cos b \cos c). \quad (3)$$ Applying the cosine theorem in
triangle $BOC$, I shall obtain the measure of $\angle BOC$, which
is given by: $$BC^2 = BO^2 + CO^2 - 2 BO\times CO \cos a = 2(1 -
\cos a). \quad (4)$$ From (3) and (4) we get Pythagoras' Theorem on
the sphere: $$\cos a = \cos b \cos c.$$ An alternative proof of
Pythagoras' Theorem on the sphere uses scalar products as
follows.
Since ${\bf OA, OB}$ and ${\bf OC}$ are unit vectors, the
angles between the vectors, and hence the lengths of the sides of
triangle $ABC$, are given from the scalar products: $$\eqalign{ a
&=\cos^{-1}{\bf OB.OC}= \cos^{-1}\sin u \sin v\cr b &=
\cos^{-1}{\bf OA.OC}= \cos^{-1}\sin v\cr c &= \cos^{-1}{\bf
OB.OA}= \cos^{-1}\sin u.}$$ Hence $$\cos a = \cos b \cos c.$$ For
the second part of the problem I observe that the triangle with
vertex coordinates (0, 0, 1), (0, 1, 0) and (1, 0, 0) has 3 right
angles. The lengths of its sides are all $\pi/2$. Now I shall prove
that all spherical triangles with 3 right angles are equilateral of
side $\pi/2$. All the following relations follow from the version
of Pythagoras Theorem proved above as angles $A = B = C = \pi/2$.
\begin{eqnarray} \cos a &= \cos b \cos c. \quad (5)\\ \cos b
&= \cos c \cos a. \quad (6)\\ \cos c &= \cos a \cos b.
\quad (7)\\ \end{eqnarray} Multiplying (5), (6) and (7), I obtain:
$$\cos a \cos b \cos c = (\cos a \cos b \cos c)^2.$$ If $\cos a,
\cos b, \cos c \neq 0$, then $\cos a \cos b \cos c = 1$. But $-1
\leq \cos a, \cos b, \cos c \leq 1.$ So, $\cos a= \cos b = \cos c =
1$, which means $a = b = c = 0$ (impossible) or $\cos a = \cos b =
-1$ and $\cos c = 1$ (or any other combination of $a, b$ and $c$),
which is also impossible.
So, one of $\cos a, \cos b$ or $\cos c$ is 0. Now, evidently
$\cos a = \cos b = \cos c = 0$, so $a = b = c = \pi /2$, and all
triangles with this property are congruent.
You may also like
Flexi Quads
A quadrilateral changes shape with the edge lengths constant. Show the scalar product of the diagonals is constant. If the diagonals are perpendicular in one position are they always perpendicular?
Flexi Quad Tan
As a quadrilateral Q is deformed (keeping the edge lengths constnt) the diagonals and the angle X between them change. Prove that the area of Q is proportional to tanX.
Air Routes
Find the distance of the shortest air route at an altitude of 6000 metres between London and Cape Town given the latitudes and longitudes. A simple application of scalar products of vectors.

