Skip over navigation
Jacob (Tunbridge Wells Grammar School for Boys) worked out that it had turned 120 degrees:
"83.3 recurring and this represents the number of turns. 83.3 recurring turns is the same as 83 1/3 turns. Each full turn returns the dot to the starting point, and so the point finished 120 degrees anti-clockwise from its starting position."
Nikolaus then spotted that the point at 120 degrees has been rotated 30 degrees anticlockwise from the blue vertical line, whereas the point at 60 degrees has been rotated 30 degrees clockwise, and so this is the same height:
"When it goes 60 degrees anticlockwise it is 30 degrees (clockwise) from the 90 degrees line and 1/3 of a turn is 120 degrees which is 30 degrees (anticlockwise) from the blue 90 degree line, and as the circle is symmetrical this is the same vertical height from the horizontal axis."
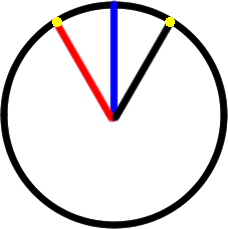
Alternatively, for those of you who may have met trigonometry, Rafael spotted that the distance from the dot to the horizontal axis is actually the sine function, and so knew that sin60=sin120, so the heights were the same.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Round and Round and Round
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Jacob (Tunbridge Wells Grammar School for Boys) worked out that it had turned 120 degrees:
"83.3 recurring and this represents the number of turns. 83.3 recurring turns is the same as 83 1/3 turns. Each full turn returns the dot to the starting point, and so the point finished 120 degrees anti-clockwise from its starting position."
Nikolaus then spotted that the point at 120 degrees has been rotated 30 degrees anticlockwise from the blue vertical line, whereas the point at 60 degrees has been rotated 30 degrees clockwise, and so this is the same height:
"When it goes 60 degrees anticlockwise it is 30 degrees (clockwise) from the 90 degrees line and 1/3 of a turn is 120 degrees which is 30 degrees (anticlockwise) from the blue 90 degree line, and as the circle is symmetrical this is the same vertical height from the horizontal axis."

Alternatively, for those of you who may have met trigonometry, Rafael spotted that the distance from the dot to the horizontal axis is actually the sine function, and so knew that sin60=sin120, so the heights were the same.
You may also like
Matching Fractions, Decimals and Percentages
Can you match pairs of fractions, decimals and percentages, and beat your previous scores?


