Skip over navigation
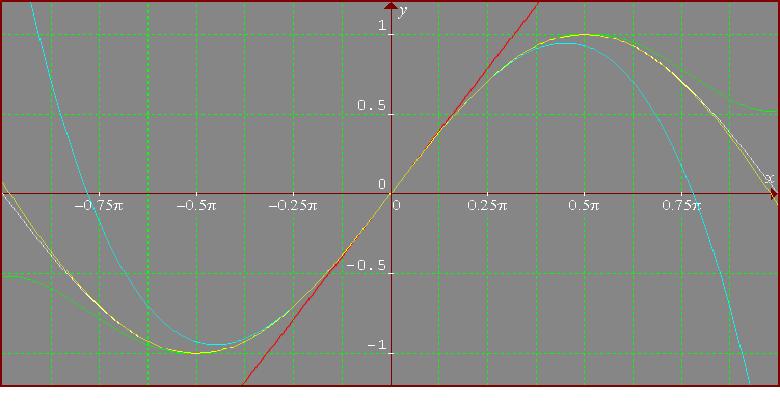
The function sin(x) is represented in white, the first order polynomial in red, the third in cyan, the fifth in green and the seventh in yellow. It can be observed that the accuracy is better and better. As the order of the polynomial increases, the accuracy increases.
It is remarkable that, using only up to the seventh order polynomial, I obtain a very good approximation of the function. Sin is a periodic function and so it is sufficient to work on the interval $[-\pi, \pi]$, and, observing that sin is an odd function the interval $[0, \pi]$ is enough. Around $\pi$, in fact I should use the expansion of the function around this value. This is equivalent to moving the y-axis $\pi$ to the right.
I work in a similar manner for $\cos x$ and $\log (1+x).$ For $\cos x$, the MacLaurin series expansion is: $$\cos x = 1 - {x^2\over 2!} + {x^4\over 4!} - {x^6\over 6!} +...$$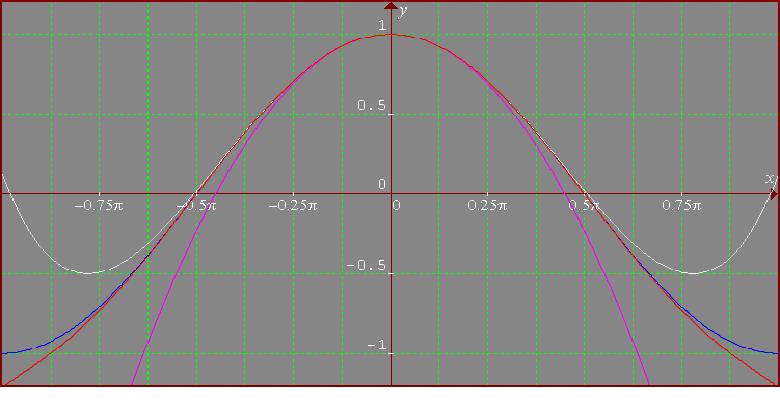
The function is in blue, the second order polynomial in violet, the fourth - in white and the sixth in red. I see that the sixth order polynomial is a rather good approximation on the whole interval.
As cos is periodic, the interval $[-\pi, \pi]$ is sufficient, and more, as cos(x) is even $[0, \pi]$ is enough.
For, $\log (1+x)$, I consider the logarithm to the base e. Here, I obtain the following MacLaurin series expansion: $$\log (1+x) = x - {x^2\over 2} + {x^3\over 3} - {x^4\over 4} + {x^5\over 5} ...$$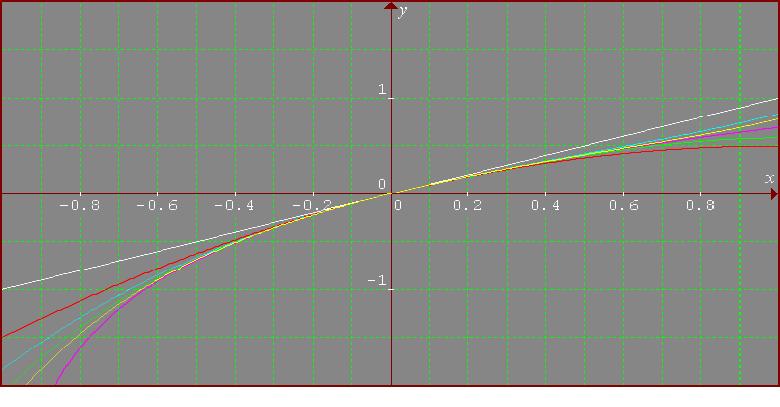
Here, the colours of the curves are as follows: violet for the function, white for the first order approximation, red for the second, cyan for the third, green for the fourth and yellow for the fifth.
In this case, the approximations are good only on a small interval around the origin. I think that for approximations of the function valid on different intervals, I have to use the series expansion around the chosen point. So, around x=1: $$\log (1 + x) = \log 2 + {x-1\over 2} - {(x-1)^2\over 2^3} + {(x-1)^3\over 24} - {(x-1)^4\over 64} + {(x-1)^5\over 160}1 ...$$
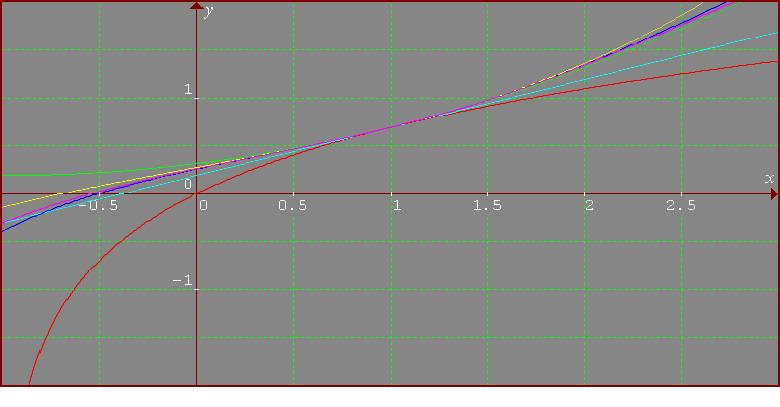
The colours are as follows: the function in red, the first order polynomial in cyan, the second order one in green, the third in yellow, the fourth in blue, and the fifth in violet.
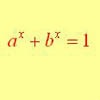
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Building Approximations for Sin(x)
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Aleksander from Gdynia Bilingual High School No 3, Poland used the properties of the sine function to find a polynomial approximation.
As we know, polynomials are one of the most flexible functions
and hence, can have very different shapes. They are probably the
most flexible functions you can find, thus we can state a
hypothesis that every function can be approximated by a polynomial
of an appropriately high degree. Let's now consider sine, the
functions that is very difficult to calculate and thus we usually
need its approximation. In the beginning let's find coefficients in
the following expression: $$\sin x \approx a + bx +cx^2 +dx^3.$$
Let's make a few observations:
(1) Sine is an odd function
(2) $\sin [0]=0$
(3) For sufficiently small $x$, $\sin x \approx x$.
Polynomials are odd only if coefficients of even powers of $x$
are equal to 0.
From the statements above we have:
$\sin (0) = 0 \Rightarrow a=0$
From (3), $b=1$\\ From (1), $c=0$.
After simplification $\sin x \approx x +dx^3$. Taking $x =
{\pi \over 6}$ and $\sin x = 0.5$ a simple calculation gives $d = -
0.1643968$ which is close to $d = -{1\over 6}$ and we have $\sin x
\approx x - {x^3 \over 6}$.
To get approximation of $\sin x$ using polynomials of higher
degrees, we have to remember that coefficients of even powers
should be equal to 0. For that reason the next degree of a
polynomial that can be used here is the 5th.
Andrei from Romania used the Taylor series and drew graphs to show the polynomial approximations .
To solve this problem, I use the Taylor series expansion around the origin. I see that the derivatives of $f(x) = \sin x $ are: $$\eqalign{ f^{4k}(x) &= \sin x \cr f^{4k+1}(x) &= \cos x \cr f^{4k+2}(x) &= -\sin x \cr f^{4k+3}(x) &= -\cos x }.$$ The formula for the Taylor expansion is: $$f(x) = f(x_0) + {(x - x_0)\over 1!}f'(x_0)+ {(x - x_0)^2\over 2!}f''(x_0)+... + {(x - x_0)^k\over k!}f^{(k)}(x_0)+ ...$$ Evidently, the odd-order derivatives are 0 for $x_0=0$. So, $\sin x$ could be written around the origin as: $$\sin x = x - {x^3\over 3!} + {x^5\over 5!} - {x^7\over 7!} + ...$$ The simplest method to test the accuracy of the series expansion is to represent on the same graph the function and its different order expansions.The function sin(x) is represented in white, the first order polynomial in red, the third in cyan, the fifth in green and the seventh in yellow. It can be observed that the accuracy is better and better. As the order of the polynomial increases, the accuracy increases.
It is remarkable that, using only up to the seventh order polynomial, I obtain a very good approximation of the function. Sin is a periodic function and so it is sufficient to work on the interval $[-\pi, \pi]$, and, observing that sin is an odd function the interval $[0, \pi]$ is enough. Around $\pi$, in fact I should use the expansion of the function around this value. This is equivalent to moving the y-axis $\pi$ to the right.
I work in a similar manner for $\cos x$ and $\log (1+x).$ For $\cos x$, the MacLaurin series expansion is: $$\cos x = 1 - {x^2\over 2!} + {x^4\over 4!} - {x^6\over 6!} +...$$
The function is in blue, the second order polynomial in violet, the fourth - in white and the sixth in red. I see that the sixth order polynomial is a rather good approximation on the whole interval.
As cos is periodic, the interval $[-\pi, \pi]$ is sufficient, and more, as cos(x) is even $[0, \pi]$ is enough.
For, $\log (1+x)$, I consider the logarithm to the base e. Here, I obtain the following MacLaurin series expansion: $$\log (1+x) = x - {x^2\over 2} + {x^3\over 3} - {x^4\over 4} + {x^5\over 5} ...$$
Here, the colours of the curves are as follows: violet for the function, white for the first order approximation, red for the second, cyan for the third, green for the fourth and yellow for the fifth.
In this case, the approximations are good only on a small interval around the origin. I think that for approximations of the function valid on different intervals, I have to use the series expansion around the chosen point. So, around x=1: $$\log (1 + x) = \log 2 + {x-1\over 2} - {(x-1)^2\over 2^3} + {(x-1)^3\over 24} - {(x-1)^4\over 64} + {(x-1)^5\over 160}1 ...$$
The colours are as follows: the function in red, the first order polynomial in cyan, the second order one in green, the third in yellow, the fourth in blue, and the fifth in violet.
You may also like
What Do Functions Do for Tiny X?
Looking at small values of functions. Motivating the existence of the Taylor expansion.
Equation Attack
The equation a^x + b^x = 1 can be solved algebraically in special cases but in general it can only be solved by numerical methods.

