Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Knights Moving



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
While it may be tempting, and fun, to simply try to do the puzzle as it for a while, there is a rather nice way of simplifying the problem.
By joining up each of the squares that are connected by a knights move, we can reduce the problem down to a graph, where the knights can move along connected nodes.
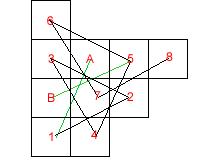
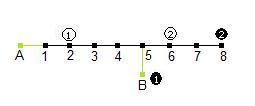
The graph turns out to be rather simple! All of the squares end up on a single line, with the single square 'B' branching off.
Clearly, by moving the pieces along one node at a time, the only place where any swapping can happen is at B. The quickest way would be to swap W1 and B1 , and swap W2 and B2 (otherwise there would be even more swapping. There are two ways of doing this:
Swapping W1 and B1, then W2 and B2:
- W2: 6 to 7
- W1: 2 to 6
- B1: B to 2
- W1: 6 to 3 (we've now swapped W1 and B1, making room for the next swap)
- W2: 7 to B
- B2: 8 to 4
- W2: B to 8
- B2: 4 to 6.
- W1: 3 to B. Done! 28 moves
Swapping W2 and B2, then W1 and B1:
- B1: B to 3
- W2: 6 to B
- B2: 8 to 4
- W2: B to 8
- B2: 4 to 7 (we've swapped W2 and B2, making room for the next swap)
- B1: 3 to 6
- W1: 2 to B
- B1: 6 to 2 (we've now swapped W1 and B1)
- B2: 7 to 6. Done! 28 moves
So the minimum number of moves is 28.
You may also like
A Knight's Journey
This article looks at knight's moves on a chess board and introduces you to the idea of vectors and vector addition.

