Skip over navigation
The triangles in this set are 'similar':
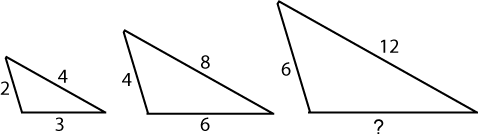
'Similar' means that the triangles are exactly the same shape, but not the same size. The sides are in the same ratio to each other. (Note that these triangles are not drawn to scale.)
What can you say about the length of the side of the third triangle which is marked with a question mark? Of course the triangles could be different ways up, too:
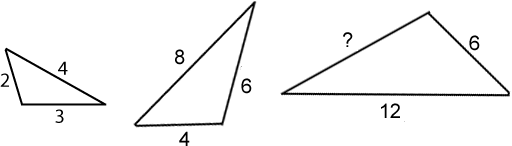
There are five more sets of similar triangles below. Can you work out the lengths of the sides marked with a question mark?
Set 2:
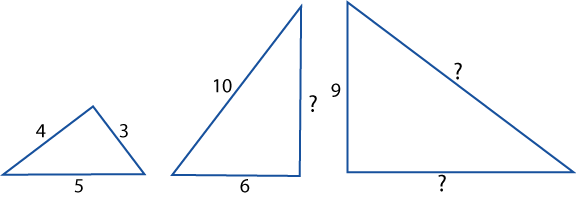
Set 3:
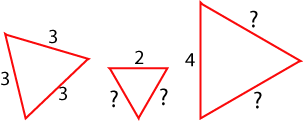
Set 4:
Set 5:
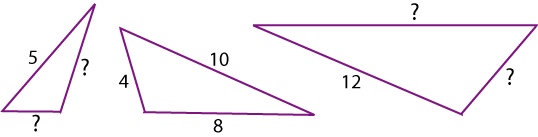
Set 6:
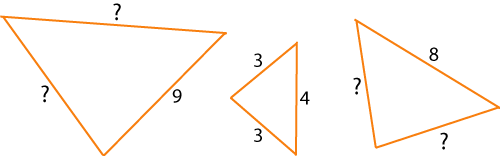
Learners could draw their own sets of similar triangles.
Suggest using the interactivity in this simpler problem which introduces similar triangles.
Number the Sides
Age 7 to 11
Challenge Level 
Number the Sides
The triangles in this set are 'similar':
'Similar' means that the triangles are exactly the same shape, but not the same size. The sides are in the same ratio to each other. (Note that these triangles are not drawn to scale.)
What can you say about the length of the side of the third triangle which is marked with a question mark? Of course the triangles could be different ways up, too:
There are five more sets of similar triangles below. Can you work out the lengths of the sides marked with a question mark?
Set 2:
Set 3:
Set 4:
Set 5:
Set 6:
Why do this problem?
This problem is a good introduction to the numerical aspects of similar triangles. It will also bring in ratio, and use multiplication and division.
Possible approach
You might suggest that children have a go at the Matching Triangles problem before they try this, which would offer a good basic introduction to similar triangles and might provoke some interesting discussion amongst the class.
This problem would be best introduced to the whole group at first. You could simply show them the first three triangles and ask them what they think the missing length is. Invite children to explain to everyone how they worked out their response. Listening to different ways of articulating the thought processes will help those who are not so sure find an explanation which they can make their
own. The next step might be to show the group the same set of triangles but with the third triangle in a different orientation as in the second image. This will challenge them a little at first but makes a good lead into the main activity.
You could print off copies of this sheet for the children to use, which has all the sets of triangles on it.
Key questions
Would it help to write out the lengths of the sides of each triangle in a set?
Why don't you compare the shortest side of the first triangle with the shortest side of the third triangle?
How about comparing the two "middle length" sides?
Can you use this to work out what the longest side length is in the third triangle?
Possible extension
Learners could draw their own sets of similar triangles.
Possible support
Suggest using the interactivity in this simpler problem which introduces similar triangles.You may also like
Is a Square a Rectangle?
How many rectangles can you find in this shape? Which ones are differently sized and which are 'similar'?