Number the Sides

Many of you sent in answers to this problem, but not many of you explained how you arrived at the answers. It can be hard to put into words what you did, but if you try to explain, you often find you end up understanding what you did much better.

Sophie from Haywards Primary School was one of the few people who gave us some detail about what she did. She says:

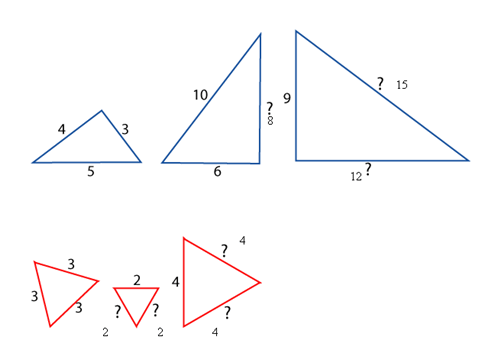
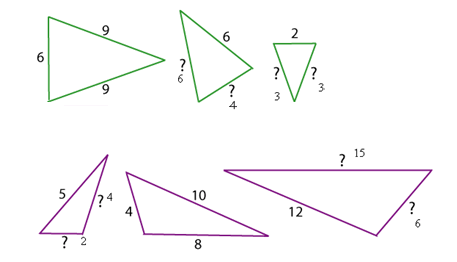
Set two:
Times the first length of the triangle by 2 for the second and then add it again to get the answers of the third triangle so the answer is 8, 12 and 15

Set three:
All the lengths are the same so the answer is 2, 2, 4 and 4

Set four:
Two thirds of the first length for the second triangle and then one third for the third triangle so the answer is 6, 4, 3 and 3
Set five:
For the first triangle you half the length of the second triangle and you add the length that is half of the second triangle so the answer is 2, 4, 6 and 15

Set six:

Times the 3 to get to 9 so you times the 4 to get 12 so the answer is 9, 9 and 12
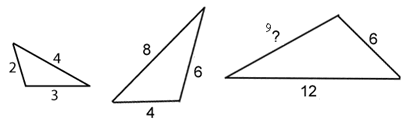
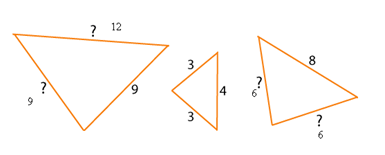
Times the 4 by 2 to get 8 so times the 3 by 2 you get 6 so the answer is 8, 6 and 6

Perhaps you can expand on what Sophie has said? What we're interested in is why we would "times" by the amounts that Sophie has suggested. Emma from Lord Williams School talked about patterns which she could see in the lengths of the sides. This is a good way to look at it, Emma.

Daniel from Reading School sent in pictures of the triangles with their lengths labelled: