Skip over navigation
You could try Number Lines before this problem.
Max and Mandy both had number lines. Max's number line went along from left to right like this:
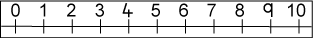
Mandy's number line went up and down like this:
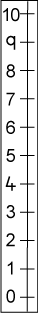
Max and Mandy both started at zero on their number lines. Max made a secret jump along his number line and then moved on seven and landed on $10$. How long was his secret jump?
Mandy made a jump of three and another secret jump. She landed on $6$. How long was her secret jump?
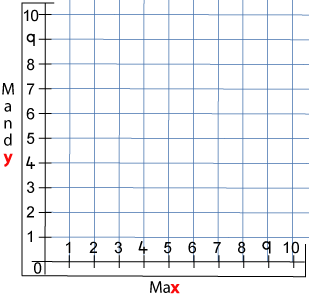
Max and Mandy decided to put their number lines together. Their teacher gave them some squared paper. They had made a graph. It looked like a bit like this:
Max moved four along and Mandy moved six up. They put a counter on the place they landed. Now their graph looked like this:
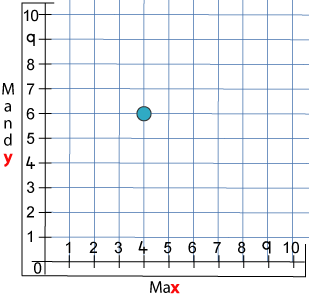
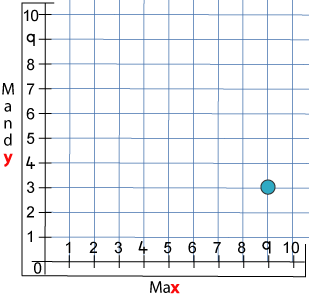
How far had each of them moved along and up from $0$ to get the counter to the place marked on the grid below?
If Max and Mandy both moved the same distance along and up, where could the counter be?
Two Number Lines
Age 7 to 11
Challenge Level 
You could try Number Lines before this problem.
Max and Mandy both had number lines. Max's number line went along from left to right like this:
Mandy's number line went up and down like this:
Max and Mandy both started at zero on their number lines. Max made a secret jump along his number line and then moved on seven and landed on $10$. How long was his secret jump?
Mandy made a jump of three and another secret jump. She landed on $6$. How long was her secret jump?
Max and Mandy decided to put their number lines together. Their teacher gave them some squared paper. They had made a graph. It looked like a bit like this:
Max moved four along and Mandy moved six up. They put a counter on the place they landed. Now their graph looked like this:
How far had each of them moved along and up from $0$ to get the counter to the place marked on the grid below?
If Max and Mandy both moved the same distance along and up, where could the counter be?
You may also like
Prompt Cards
These two group activities use mathematical reasoning - one is numerical, one geometric.
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.